Question

抛物线mx+ny²=0的顶点坐标是    ，焦点坐标是    ，准线方程是    ，离心率是    ，通径长    ．

Answer 1

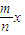
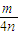
【答案】分析：先将抛物线mx+ny²=0化为标准形式y²=-，可得到顶点坐标为原点，进而可求得焦点坐标、准线方程、离心率，再令x=-代入抛物线求出y的值，根据通径的定义可得到答案．
解答：解：∵mx+ny²=0∴y²=-
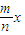
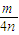
∴顶点坐标为（0，0），焦点坐标为：（-，0），准线方程为x=，
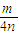
离心率e=1，
当x=-时，代入抛物线方程y=±•
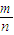
∴通径长=||
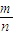
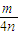
故答案为：（0，0），（-，0），x=，e=1，||．
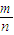
点评：本题主要考查抛物线的基本性质．属基础题．