
设函数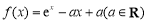 ,其图象与
,其图象与 轴交于
轴交于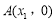 ,
,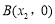 两点,且x1<x2.
两点,且x1<x2.
(1)求 的取值范围;
的取值范围;
(2)证明: (
( 为函数
为函数 的导函数);
的导函数);
(3)设点C在函数 的图象上,且△ABC为等腰直角三角形,记
的图象上,且△ABC为等腰直角三角形,记 ,求
,求
的值.
(1)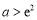 ;(2)详见解析;(3)
;(2)详见解析;(3)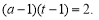
【解析】
试题分析:(1)根据题意图象与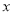 轴交于
轴交于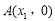 ,
,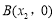 两点,由零点的定义可得:函数的图象要与x轴有两个交点,而此函数的特征不难发现要对它进行求导,运用导数与函数的关系进行求函数的性质,即:
两点,由零点的定义可得:函数的图象要与x轴有两个交点,而此函数的特征不难发现要对它进行求导,运用导数与函数的关系进行求函数的性质,即: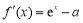 ,a的正负就决定着导数的取值情况,故要对a进行分类讨论:分
,a的正负就决定着导数的取值情况,故要对a进行分类讨论:分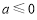 和
和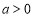 两种情况,其中
两种情况,其中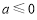 显然不成立,
显然不成立,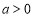 时转化为函数的最小值小于零,即可求出a的范围; (2)由图象与
时转化为函数的最小值小于零,即可求出a的范围; (2)由图象与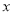 轴交于
轴交于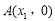 ,
,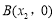 两点,结合零点的定义可得:
两点,结合零点的定义可得: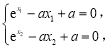 整理可得:
整理可得: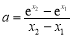 ,观察其结构特征,可想到整体思想,即:
,观察其结构特征,可想到整体思想,即: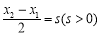 ,目标为:
,目标为: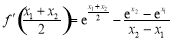 ,运用整体代入化简可得:
,运用整体代入化简可得: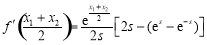 ,转化为对函数
,转化为对函数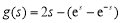 进行研究,运用导数知识不难得到
进行研究,运用导数知识不难得到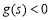 ,即:
,即: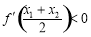 ,故而
,故而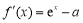 是单调增函数,由不等式知:
是单调增函数,由不等式知: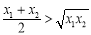 ,问题可得证; (3)由题意有
,问题可得证; (3)由题意有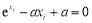 ,化简得
,化简得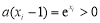
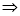
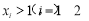 ,而在等腰三角形ABC中,显然只有C = 90°,这样可得
,而在等腰三角形ABC中,显然只有C = 90°,这样可得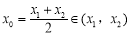 ,即
,即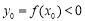 ,结合直角三角形斜边的中线性质,可知
,结合直角三角形斜边的中线性质,可知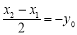 ,所以
,所以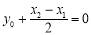 ,即
,即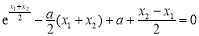 ,运用代数式知识处理可得:
,运用代数式知识处理可得: 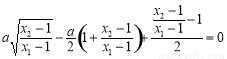 ,而
,而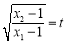 ,所以
,所以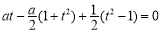 ,即
,即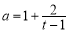 ,所求得
,所求得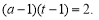
试题解析:(1)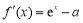 .
.
若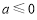 ,则
,则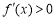 ,则函数
,则函数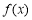 是单调增函数,这与题设矛盾. 2分
是单调增函数,这与题设矛盾. 2分
所以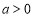 ,令
,令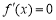 ,则
,则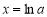 .
.
当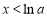 时,
时,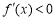 ,
,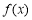 是单调减函数;
是单调减函数;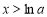 时,
时,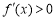 ,
,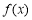 是单调增函数;
是单调增函数;
于是当 时,
时,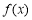 取得极小值. 4分
取得极小值. 4分
因为函数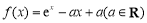 的图象与
的图象与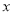 轴交于两点
轴交于两点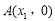 ,
,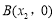 (x1<x2),
(x1<x2),
所以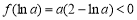 ,即
,即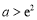
此时,存在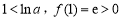 ;
;
存在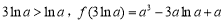
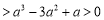 ,
,
又由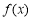 在
在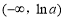 及
及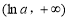 上的单调性及曲线在R上不间断,可知
上的单调性及曲线在R上不间断,可知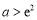 为所求取值范围. 6分
为所求取值范围. 6分
(2)因为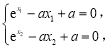 两式相减得
两式相减得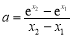
记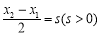 ,则
,则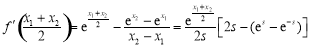 , 8分
, 8分
设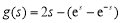 ,则
,则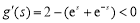 ,所以
,所以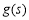 是单调减函数,
是单调减函数,
则有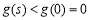 ,而
,而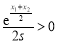 ,所以
,所以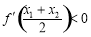 .
.
又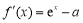 是单调增函数,且
是单调增函数,且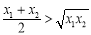
所以 . 11分
. 11分
(3)依题意有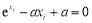 ,则
,则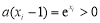
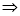
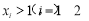 .
.
于是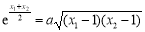 ,在等腰三角形ABC中,显然C = 90°, 13分
,在等腰三角形ABC中,显然C = 90°, 13分
所以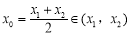 ,即
,即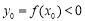 ,
,
由直角三角形斜边的中线性质,可知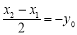 ,
,
所以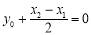 ,即
,即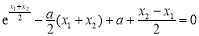 ,
,
所以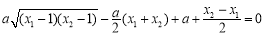 ,
,
即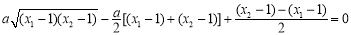 .
.
因为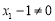 ,则
,则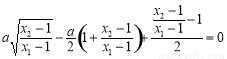 ,
,
又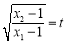 ,所以
,所以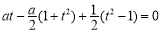 , 15分
, 15分
即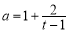 ,所以
,所以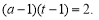 16分
16分
考点:1.函数的图象性质;2.导数在函数中的运用;3.函数与不等式的综全运用


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年江苏省高考模拟考试文科数学试卷(解析版) 题型:填空题
若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为2 cm的半圆,则该圆锥的体积为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:解答题
在长方体ABCD—A1B1C1D1中,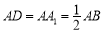 ,点E是棱AB上一点.且
,点E是棱AB上一点.且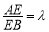 .
.

(1)证明: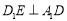 ;
;
(2)若二面角D1—EC—D的大小为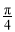 ,求
,求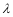 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:填空题
设l,m表示直线,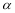 表示平面,m是
表示平面,m是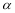 内任意一条直线.则“
内任意一条直线.则“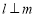 ”是“
”是“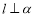 ”成立的 条件.(在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选填一个)
”成立的 条件.(在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选填一个)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆
弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧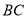 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
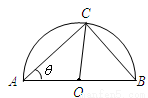
(1)设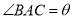 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为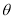 的函数
的函数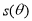 ;
;
(2)试确定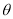 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
已知矩阵A=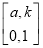 (k≠0)的一个特征向量为α=
(k≠0)的一个特征向量为α=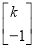 ,A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1).求实数a,k的值.
,A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1).求实数a,k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com