练习册

  • 练习册
  • 试题
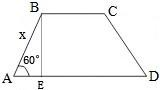
    精英家教网 > 高中数学 > 题目详情
    等腰梯形的周长为60，底角为60°，问这梯形各边长为多少时，面积最大？
    精英家教网
    分析：设等腰梯形的腰长为x，利用x表达出梯形的面积，转化为求函数的最值问题．
    解答：解：设等腰梯形的腰长为x，（0＜x＜30），则有
    AE=
    x
    2
    ，BE=
    		3
    x
    2
    ，BC=
    60-2•AB-2AE
    2
    =
    60-2x-x
    2
    =
    60-3x
    2
    ．
    等腰梯形ABCD的面积=
    BC+AD
    2
    •BE
    =（BC+AE）•BE
    =(
    60-3x
    2
    +
    x
    2
    )•
    		3
    2
    x
    =
    		3
    2
    (30x-x2)
    =
    		3
    2
    [225-(x-15)2]    ．
    由此可知，当且仅当x=15时等腰梯形的面积最大．此时，腰AB=CD=x=15，上底BC=7.5，
    下底AD=BC+2AE=22.5．
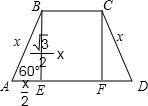
    精英家教网
    点评：本题考查函数的应用，求函数关系式和最值，难度不大，要充分结合图形表达各边长．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

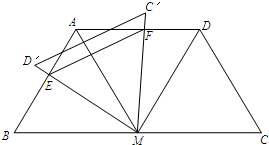    （2012•大丰市一模）已知：如图，M是线段BC的中点，BC=4，分别以MB、MC为边在线段BC的同侧作等边△BAM、等边△MCD，连接AD．
    （1）求证：四边形ABCD是等腰梯形；
    （2）将△MDC绕点M逆时针方向旋转α（60°＜α＜120°），得到△MD′C′，MD′交AB于点E，MC′交AD于点F，连接EF．
    ①求证：EF∥D′C′；
    ②△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高一版(A必修1)　2009－2010学年　第10期　总166期 人教课标高一版 题型：044

    某地兴修水利挖渠，其渠道的横截面为等腰梯形，腰与水平线的夹角为60°，要求横截面的周长为定值m(不包括上底长)．问渠深h为多少时，可使渠道的流量最大？

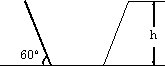
    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省高一下学期期中考试数学试卷（解析版） 题型：解答题

    建造一断面为等腰梯形的防洪堤（如图），梯形的腰与底边所角为60°，考虑到防洪堤坚固性及石块用料等因素，设计其断面面积为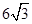m2，为了使堤的上面与两侧面的水泥用料最省，要求断面的外周长（梯形的上底BC与两腰长的和）最小．如何设计防洪堤，才能使水泥用料最省．

     

     

    查看答案和解析>>

    科目：高中数学 来源：1977年上海市高考数学试卷（理科）（解析版） 题型：解答题

    等腰梯形的周长为60，底角为60°，问这梯形各边长为多少时，面积最大？

    查看答案和解析>>

    同步练习册答案