
【题目】大学生村官王善良落实政府“精准扶贫”精神,帮助贫困户张三用9万元购进一部节能环保汽车,用于出租.假设第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该车每年的运营收入均为11万元.若该车使用了n(n∈N*)年后,年平均盈利额达到最大值,则n等于(注:年平盈利额=(总收入﹣总成本)× ![]() )( )
)( )
A.3
B.4
C.5
D.6
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx﹣ ![]() )(
)( ![]() <ω<2),在区间(0,
<ω<2),在区间(0, ![]() )上( )
)上( )
A.既有最大值又有最小值
B.有最大值没有最小值
C.有最小值没有最大值
D.既没有最大值也没有最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,a2=6,且数列{an﹣1﹣an}{n∈N*}是公差为2的等差数列.
(1)求{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 求满足不等式Sn>
}的前n项和为Sn , 求满足不等式Sn> ![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、 
(1)设AD=x,将矩形ABCD的面积y表示成x的函数,并写出其定义域;
(2)怎样截取,才能使矩形材料ABCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,AB=2,点E是BC的中点. 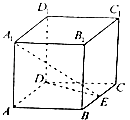
(1)求线段DE的长;
(2)求直线A1E与平面ADD1A1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:θ为第一象限角, ![]() =(sin(θ﹣π),1),
=(sin(θ﹣π),1), ![]() =(sin(
=(sin( ![]() ﹣θ),﹣
﹣θ),﹣ ![]() ),
),
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)若| ![]() +
+ ![]() |=1,求sinθ+cosθ的值.
|=1,求sinθ+cosθ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com