
 。
。
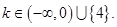
解析试题分析:由题意,当k>0时,函数定义域是(0,+∞),当k<0时,函数定义域是(-1,0)
当k>0时,lgkx=2lg(x+1),∴lgkx-2lg(x+1)=0
∴lgkx-lg(x+1)2=0,即kx=(x+1)2在(0,+∞)仅有一个解
∴x2-(k-2)x+1=0在(0,+∞)仅有一个解
令f(x)=x2-(k-2)x+1,
又当x=0时,f(x)=x2-(k-2)x+1=1>0
∴△=(k-2)2-4="0," ∴k-2="±2," ∴k=0舍,或4
k=0时lgkx无意义,舍去 , ∴k=4
当k<0时,函数定义域是(-1,0)
函数y=kx是一个递减过(-1,-k)与(0,0)的线段,函数y=(x+1)2在(-1,0)递增且过两点(-1,0)与(0,1),此时两曲线段恒有一个交点,故k<0符合题意,
综上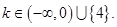
考点:根的存在性及根的个数判断;对数函数的图像与性质.
点评:本题主要考查在对数方程的应用,要按照解对数方程的思路熟练应用对数的性质及其运算法则转化问题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:填空题
定义在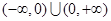 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称 为“等比函数”。现有定义在
为“等比函数”。现有定义在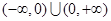 上的如下函数:①
上的如下函数:① ;②
;② ;③
;③ ;④
;④ ,则其中是“等比函数”的
,则其中是“等比函数”的 的序号为
的序号为
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
为了在“十一”黄金周期间降价搞促销,某超市对顾客实行购物优惠活动,规定一次购物付款总额:(1)如果不超过200元,则不予优惠;(2)如果超过200元,但不超过500元,则按标价给予9折优惠;(3)如果超过500元,其中500元按第(2)条给予优惠,超过500元的部分给予7折优惠。小张两次去购物,分别付款168元和423元,假设她一次性购买上述同样的商品,则应付款额为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com