练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图，M(－2，0)和N(2，0)是平面上的两点，动点P满足：||PM|－|PN||＝2．

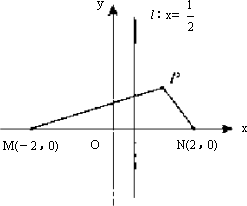
    (Ⅰ)求点P的轨迹方程；

    (Ⅱ)设d为点P到直线l：的距离，若|PM|＝2|PN|2，求的值．

    答案：
    解析：

    　　解：(Ⅰ)由双曲线的定义，点P的轨迹是以M、N为焦点，实轴长2a＝2的双曲线．

    　　因此半焦距c＝2，实半轴a＝1，从而虚半轴b＝，

    　　所以双曲线的方程为x2－＝1．

    　　(Ⅱ)解法一：

    　　由(Ⅰ)由双曲线的定义，点P的轨迹是以M、N为焦点，实轴长2a＝2的双曲线．

    　　因此半焦距e＝2，实半轴a＝1，从而虚半轴b＝．

    　　R所以双曲线的方程为x2－＝1．

    　　(Ⅱ)解法一：

    　　由(Ⅰ)及下图，易知|PN|1，因|PM|＝2|PN|2，　　①

    　　知|PM|＞|PN|，故P为双曲线右支上的点，所以|PM|＝|PN|＋2．　　②

    　　将②代入①，得2||PN|2－|PN|－2＝0，解得|PN|＝，所以|PN|＝．

    　　因为双曲线的离心率e＝＝2，直线l：x＝是双曲线的右准线，故＝e＝2，

    　　所以d＝|PN|，因此

    　　

    　　解法：

    　　设P(x，y)，因|PN|1知|PM|＝2|PN|22|PN|＞|PN|，

    　　故P在双曲线右支上，所以x1．

    　　由双曲线方程有y2＝3x2－3．

    　　因此

    　　

    　　从而由|PM|＝2|PN|2得

    　　2x＋1＝2(4x2－4x＋1)，即8x2－10x＋1＝0．

    　　所以x＝(舍去x＝)．

    　　有|PM|＝2x＋1＝

    　　d＝x－＝．

    　　故


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•中山一模）函数f（x）=2sin（ωx+φ）(ω＞0，0＜φ＜
    π
    2
    )    的部分图象如下图所示，该图象与y轴交于点F（0，1），与x轴交于点B，C，M为最高点，且三角形MBC的面积为π．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）若f(α-
    π
    6
    )=
    2
    		5
    5
    ，α∈(0，
    π
    2
    )    ，求cos(2α+
    π
    4
    )    的值．

    查看答案和解析>>

    科目：高中数学 来源：2010年重庆市西南师大附中高二上学期期中考试理科数学卷 题型：解答题

    (本小题满分12分)
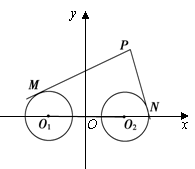
    如下图，O1（– 2，0），O2（2，0），圆O1与圆O2的半径都是1，
     
     
     

    (1)   过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点)，使得．求动点P的轨迹方程；
    (2)   若直线交圆O2于A、B，又点C（3，1），当m取何值时，△ABC的面积最大？

    查看答案和解析>>

    科目：高中数学 来源：2010年重庆市高二上学期期中考试理科数学卷 题型：解答题

    (本小题满分12分)

    如下图，O1（– 2，0），O2（2，0），圆O1与圆O2的半径都是1，

     

     

     

     

     

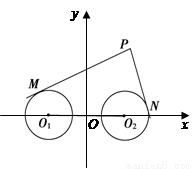
    (1)    过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点)，使得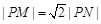．求动点P的轨迹方程；

    (2)    若直线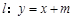交圆O2于A、B，又点C（3，1），当m取何值时，△ABC的面积最大？

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (本小题满分12分)

    如下图，O1（– 2，0），O2（2，0），圆O1与圆O2的半径都是1，

    过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点)，使得．求动点P的轨迹方程；

    若直线交圆O2于A、B，又点C（3，1），当m取何值时，△ABC的面积最大？

    查看答案和解析>>

    同步练习册答案