已知顶点为原点O,焦点在x轴上的抛物线,其内接△ABC的重心是焦点F,若直线BC的方程为4x+y-20=0.
(1)求抛物线方程;
(2)轴上是否存在定点M,使过M的动直线与抛物线交于P,Q两点,满足∠POQ=90°?证明你的结论.
分析:(1)先设抛物线方程为y
2=4px,然后表示出焦点坐标,抛物线和直线方程联立可消去y得到4x
2-(p+40)x+100=0,进而可得到B,C的横坐标之和与纵坐标之和,再由A点在抛物线上得到坐标满足抛物线方程,最后将A,B,C的坐标代入△ABC重心坐标公式可求得p的值,从而确定抛物线方程.
(2)先设点M、P、Q的坐标:
①当直线斜率不存在时构造向量
、
,然后根据∠POQ=90°得到两向量的数量积等于0可得到M的坐标;
②当斜率存在时,构造直线方程然后与抛物线联立消去x,可以得到两根之和、两根之积,同样构造向量
、
,然后根据∠POQ=90°得到两向量的数量积等于0,可得到M的坐标.
解答:解:(1)设抛物线的方程为y
2=4px,则其焦点为(p,0)
与直线方程4x+y-20=0联立,有:(-4x+20)
2=4px
∴4x
2-(p+40)x+100=0,且y=-4x+20
该方程的解为B,C两点的坐标(x
2,y
2),(x
3,y
3)
x
2+x
3=
(1)
y
2+y
3=-4(x
2+x
3)+40=-p (2)
设A(x
1,y
1)
∵A在抛物线上
∴y
12=4px
1(3)
△ABC重心坐标为:(
,
)
∵重心为抛物线焦点
∴
=p,
=0
将(1),(2)代入,得:
x
1+
=3p,y
1-p=0
与(3)联立,三个方程,x
1,y
1,p三个未知数,可解
解得:p=4
故抛物线的方程为y
2=16x.
(2)设点M(a,b) P(x
4,y
4) Q(x
5,y
5)
①当直线L的斜率不存在时 即 x
4=x
5=a 且 a>0
则:令 y
4=4
,y
5=-4
∵∠POQ=90°∵
=(a,-4
),
=(a,4
)
∴
•=a
2-16a=0
解得:a=16 或 a=0(舍去)
②当直线L的斜率存在时,设斜率为k,则直线L的方程为:
y-b=k(x-a) (k≠0)
∴联立方程:
消去 x 得:ky
2-16y+16b-16ka=0
∴y
4+y
5=
,y
4•y
5=
∴x
4•x
5=
∵∠POQ=90°
∴
•=x
4•x
5+y
4•y
5=
+
=0
即:k
2(a
2-16a)+k(16b-2ab)+b
2=0对任意的k≠0都恒成立
∴有方程组:
且a≠0
∴解得:a=16,b=0
∴点M(16,0)
综上所述:存在定点M,使得以线段PQ为直径的圆经过坐标原点,
点M的坐标为:(16,0)
点评:本题主要考查抛物线的标准方程和直线与抛物线的联立问题.直线与圆锥曲线的联立是高考考查圆锥曲线的一种典型题型,一般作为压轴题出现.



 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案 已知椭圆C:
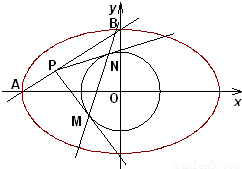
已知椭圆C:![]() ,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:
,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G: ![]() (
(![]() 是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.![]() 、
、![]() ,求椭圆C的方程;
,求椭圆C的方程;![]() 为定值时,求证:直线MN经过一定点E,并求
为定值时,求证:直线MN经过一定点E,并求![]() 的值(O是坐标原点);
的值(O是坐标原点);
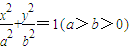 ,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:
,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G: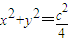 (c是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.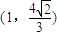 、
、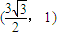 ,求椭圆C的方程;
,求椭圆C的方程;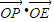 的值(O是坐标原点);
的值(O是坐标原点);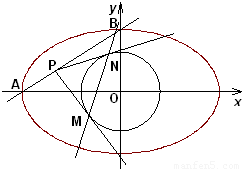
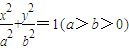 ,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:
,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G: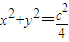 (c是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.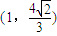 、
、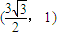 ,求椭圆C的方程;
,求椭圆C的方程;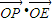 的值(O是坐标原点);
的值(O是坐标原点);