Question

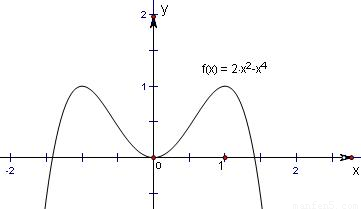
函数y=2x²-x⁴，则函数y有（ ）
A．极大值为1，极小值为0
B．极大值为1，无极小值
C．最大值为1，最小值为0
D．无极小值，也无最小值

Answer 1

【答案】分析：由y=-x⁴+2x²，知y′=-4x³+4x，x∈R，由y′=0，得x₁=-1，x₂=0，x₃=1，列表讨论，能求出函数y=2x²-x⁴的极值．
解答：解：∵y=2x²-x⁴，

∴y′=-4x³+4x，x∈R
由y′=-4x³+4x=0，得x₁=-1，x₂=0，x₃=1，
列表：

x	（-∞，-1）	-1	（-1，0）	0	（0，1）	1	（1，+∞）
f′（x）	+	0	-	0	+	0	-
f（x）	↑	极大值	↓	极小值	↑	极大值	↓

∴x=-1时，函数y=2x²-x⁴的极大值=-（-1）⁴+2（-1）²=1；
x=0时，函数y=2x²-x⁴的极小值=0⁴-2×0²=0；
x=1时，函数y=2x²-x⁴的极大值=-1⁴+2×1²=1．
故选A．
点评：本题考查函数的极大值和极小值的求法，解题时要认真审题，仔细解答，注意合理地进行等价转化．