
小明和同桌小聪一起合作探索:如图,一架5米长的梯子AB斜靠在铅直的墙壁AC上,这时梯子的底端B到墙角C的距离为1.4米.如果梯子的顶端A沿墙壁下滑0.8米,那么底端B将向左移动多少米?
(1)小明的思路如下,请你将小明的解答补充完整:
解:设点B将向左移动x米,即BE=x,则:
EC= x+1.4,DC=AC-DC=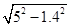 -0.8=4,
-0.8=4,
而DE=5,在Rt△DEC中,由EC2+DC2=DE2,
得方程为: , 解方程得: ,
∴点B将向左移动 米.
(2)解题回顾时,小聪提出了如下两个问题:
①将原题中的“下滑0.8米”改为“下滑1.8米”,那么答案会是1.8米吗?为什么?
②梯子顶端下滑的距离与梯子底端向左移动的距离能相等吗?为什么?
请你解答小聪提出的这两个问题.
(1)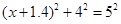 ,
,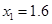
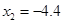 (舍去),1.6
(舍去),1.6
(2)①不会②有可能
解析试题分析:(1)根据题意及勾股定理可知,第一个空应该填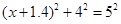 , …1分
, …1分
解方程可得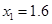 ,
,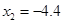 (舍去) …3分
(舍去) …3分
∴点B将向左移动 1.6 米. …4分
(2)①不会是1.8米 …5分
理由:若AD=BE=1.8,则DC=4.8-1.8=3,EC=1.4+1.8=3.2
∵3.22+ 32≠52 ∴该题的答案不会是0.9米. …7分
②有可能 …8分
理由:设梯子顶端从A处下滑a米,点B向左也移动a米,
则有(a+1.4)2+(4.8-a)2=52
解得:a =3.4或a =0(舍去).
∴当梯子顶端从A处下滑3.4米时,点B向左也移动3.4米
即:梯子顶端下滑的距离与梯子底端向左移动的距离有可能相等. …10分
考点:本小题主要考查平面几何在实际问题中的应用,考查学生应用函数知识解决实际问题的能力.
点评:解决实际问题时,要注意实际问题的定义域,还要注意灵活转化,将实际问题转化为熟悉的数学问题解决.


科目:高中数学 来源: 题型:解答题
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).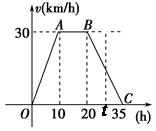
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店将进货价10元的商品按每个18元出售时,每天可卖出60个.商店经理到市场做了一番调研后发现,如将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;如将这种商品的售价(在每个18元的基础上)每降低1元,则日销售量就增加10个.为获得每日最大的利润,此商品售价应定为每个多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间有50名工人,要完成150件产品的生产任务,每件产品由3个A 型零件和1个B 型零件配套组成.每个工人每小时能加工5个A 型零件或者3个B 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一中型号的零件.设加工A 型零件的工人人数为x名(x∈N*)
(1)设完成A 型零件加工所需时间为 小时,写出
小时,写出 的解析式;
的解析式;
(2)为了在最短时间内完成全部生产任务,x应取何值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价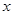 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数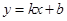 的关系(图象如下图所示).
的关系(图象如下图所示).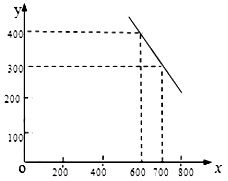
(1)根据图象,求一次函数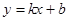 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,
①求S关于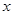 的函数表达式;
的函数表达式;
②求该公司可获得的最大毛利润,并求出此时相应的销售单价.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在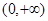 的函数
的函数 ,对任意的
,对任意的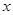 、
、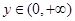 ,都有
,都有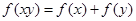 ,且当
,且当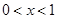 时,
时,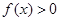 .
.
(1)证明:当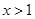 时,
时,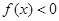 ;
;
(2)判断函数 的单调性并加以证明;
的单调性并加以证明;
(3)如果对任意的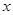 、
、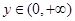 ,
,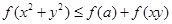 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
建造一间占 地面积为12m²的背面靠墙的猪圈,底面为长方形,猪圈正面的造价为每平方米12元,侧面的造价为每平方米80元,屋顶造价为1120元.如果墙高3m,且不计猪圈背面的费用,问:如何设计能使猪圈的总 造价最低?最低总造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com