【答案】
分析:(I)当函数为奇函数时,定义域必关于原点对称,先带着a求出函数的定义域,再根据定义域左右端点互为相反数,求出a的值.
(II)法一:先求出f
-1(x),化简f
-1(x)=m•2
-x,把m用含x的式子表示,再用均值不等式求最值即可.
法二:同法一,先化简f
-1(x)=m•2
-x,在看成关于t的一元二次方程,原方程有实解,等价于关于t的一元二次方程有正实解,在据此求出m的范围.
解答:解:(I)由

∵f(x)为奇函数,∴a-2=-a⇒a=1.
经验证可知:a=1时,f(x)是奇函数,a=1为所求
(II)∵

,∴

.
法一:由f
-1(x)=m•2
-x得:

所以m的取值范围是

法二:原方程即(2
x)
2-(m+1)2
x-m=0设2
x=t,则t
2-(m+1)t-m=0
原方程有实解,等价于方程t
2-(m+1)t-m=0有正实解
令g(t)=t
2-(m+1)t-m则


所以m的取值范围是
 点评:
点评:本题主要考查了函数奇偶性的判断,以及一元二次方程根的判断.

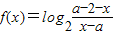 的是奇函数.
的是奇函数.
 ,∴
,∴ .
.






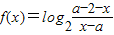 的是奇函数.
的是奇函数.