
如图所示,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3 cm,BE=7 cm.

(1)求⊙O的半径;
(2)求线段DE的长.
解:(1)连结OC.
因为MN切半圆于点C,
所以OC⊥MN.
因为AD⊥MN,BE⊥MN,
所以AD∥OC∥BE.
因为OA=OB,
所以CD=CE.
所以OC=![]() (AD+BE)=5(cm).
(AD+BE)=5(cm).
所以⊙O的半径为5 cm.
(2)连结AF.
因为AB为半圆O的直径.
所以∠AFB=90°.
所以∠AFE=90°.
又∠ADE=∠DEF=90°,
所以四边形ADEF为矩形.
所以DE=AF,AD=EF=3(cm).
在Rt△ABF中,BF=BE-EF=4 cm,AB=2OC=10(cm).
由勾股定理,得AF=![]() (cm).
(cm).
所以DE=![]() (cm).
(cm).
分析:(1)连结OC,证C为DE的中点,在解有关圆的切线问题时,常常需要作出过切点的半径.对于(2)则连结AF,证四边形ADEF为矩形,从而得到AD=EF,DE=AF,然后在Rt△ABF中运用勾股定理,求AF的长.


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
 A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,| 3π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
(2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
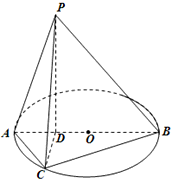 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC= AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB.查看答案和解析>>
科目:高中数学 来源:2010年新疆农七师高级中学高二第二学期第二阶段考试数学(文)试题 题型:解答题
(本题满分10)如图所示,已知AB为⊙O的直径,AC为弦,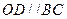 ,交AC于点D,BC=4cm,
,交AC于点D,BC=4cm,
(1)求OD的长;
(2)若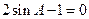 ,求⊙O的直径.
,求⊙O的直径.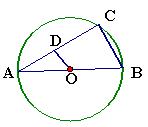
查看答案和解析>>
科目:高中数学 来源:2015届广东肇庆高二上学期期末质量检测理科数学卷(解析版) 题型:解答题
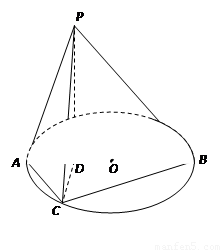
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且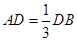 ,点C为圆O上一点,且
,点C为圆O上一点,且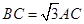 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.
(1)求证: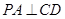 ;
;
(2)求二面角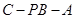 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com