
如图所示,已知AB是⊙O的直径,C为圆上任意一点,过C的切线分别与过A、B两点的切线交于P、Q.
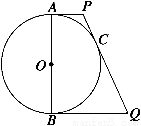
求证:AB2=4AP·BQ.
见解析
【解析】
证明 法一 连接OP、OQ,如图所示.
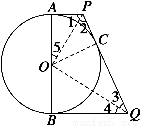
∵AP、PQ、BQ为⊙O的切线,
∴∠1=∠2,∠3=∠4.
又AP、BQ为⊙O的切线,
AB为直径,∴AB⊥AP,AB⊥BQ.
∴AP∥BQ.
∴∠A=∠B=90°,
∠1+∠2+∠3+∠4=180°.
∴∠1+∠4=∠2+∠3=90°.
∵∠1+∠5=90°,∴∠4=∠5.
∴△AOP∽△BQO.
∴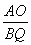 =
=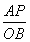 .
.
∵AB=2AO=2OB,∴AB2=4AP·BQ.
法二 连接OC.
同上可证得∠2+∠3=90°.
∵PQ切⊙O于C,∴OC⊥PQ.
在Rt△PQO中,由射影定理可得OC2=PC·CQ,
利用切线长定理,有PC=AP,BQ=QC.
OC2=AP·BQ,∵AB=2OC,∴AB2=4AP·BQ.
法三 如图所示,过P作BQ的垂线PD,垂足为D.
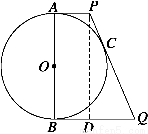
∵AP、BQ、PQ切⊙O于A、B、C,
∴∠A=∠B=90°,
AP=PC,CQ=BQ.
∴四边形ABDP为矩形,
PQ=AP+BQ.∵AP=BD,AB=PD.
在Rt△PQD中,利用勾股定理得:PQ2=PD2+QD2,
∴(AP+BQ)2=AB2+(BQ-AP)2.
∴4AP·BQ=AB2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第1课时练习卷(解析版) 题型:填空题
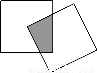
现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为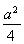 .类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为________.
.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第1课时练习卷(解析版) 题型:解答题
已知集合A={y|y=-2x,x∈[2,3]},B={x|x2+3x-a2-3a>0}.若A B,求实数a的取值范围.
B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标演练模块检测练习卷(解析版) 题型:填空题
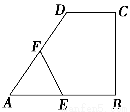
如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=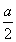 ,点E,F分别为线段AB,AD的中点,则EF=________.
,点E,F分别为线段AB,AD的中点,则EF=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标演练模块检测练习卷(解析版) 题型:选择题
如图所示,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是

A.72° B.63°
C.54° D.36°
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标检测第2讲练习卷(解析版) 题型:填空题
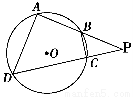
如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若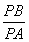 =
=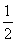 ,
,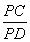 =
= ,则
,则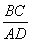 的值为______.
的值为______.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标检测第2讲练习卷(解析版) 题型:选择题
如图,锐角三形ABC内接于⊙O,∠ABC=60°,∠BAC=40°,作OE⊥AB交劣弧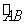 于点E,连接EC,则∠OEC=( ).
于点E,连接EC,则∠OEC=( ).

A.5° B.10°
C.15° D.20°
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标检测第1讲练习卷(解析版) 题型:填空题
如图,在△ABC中,M、N分别是AB、BC的中点,AN、CM交于点O,那么△MON与△AOC面积的比是________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-2练习卷(解析版) 题型:解答题
(拓展深化)如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.

(1)证明:B、D、H、E四点共圆;
(2)证明:CE平分∠DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com