
(2007
宁夏,21)设函数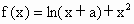 .
.
(1)
若当x=-1时f(x)取得极值,求a的值,并讨论f(x)的单调性;(2)
若f(x)存在极值,求a的取值范围,并证明所有极值之和大于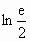 .
. |
解析: (1)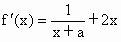 , ,
依题意有 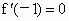 ,故 ,故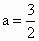 , ,
从而 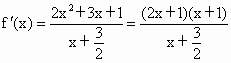 . .
f(x) 的定义域为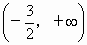 . .
当 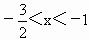 时, 时,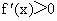 ;当 ;当 时, 时,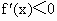 ;当 ;当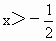 时, 时,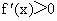 .从而,f(x)分别在区间 .从而,f(x)分别在区间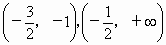 单调递增,在区间 单调递增,在区间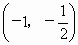 单调递减. 单调递减.
(2)f(x) 的定义域为 . .
方程 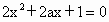 的判别式 的判别式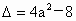 . .
(i) 若Δ<0,即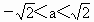 .在f(x)的定义域内 .在f(x)的定义域内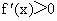 ,故f(x)无极值. ,故f(x)无极值.
(ii) 若Δ=0,则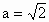 或 或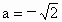 .若 .若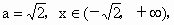
当 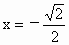 时, 时,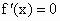 ,当 ,当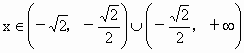 时, 时,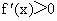 ,所以f(x)无极值. ,所以f(x)无极值.
若 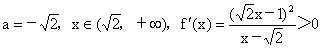 ,f(x)也无极值. ,f(x)也无极值.
(iii) 若Δ>0,即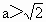 或 或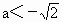 ,则 ,则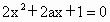 有两个不同的实根 有两个不同的实根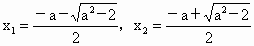 . .
当 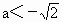 时, 时,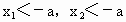 .从而 .从而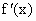 在f(x)的定义域内没有零点,故f(x)无极值. 在f(x)的定义域内没有零点,故f(x)无极值.
当 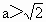 时, 时,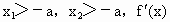 在f(x)的定义域内有两个不同的零点,由极值判别方法知f(x)在 在f(x)的定义域内有两个不同的零点,由极值判别方法知f(x)在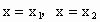 取得极值.综上,f(x)存在极值时,a的取值范围为 取得极值.综上,f(x)存在极值时,a的取值范围为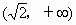 .f(x)的极值之和为 .f(x)的极值之和为
|


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com