
如下图,正方形ABCD与ABEF不在同一平面内,M、N分别在AC、BF上,且AM=FN
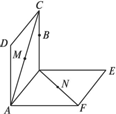
求证:MN∥平面CBE.
|
证法一:如下图,作MT∥AB交BC
于点T,作NH∥AB交BE于点H,连结HT, ∵AM=FN, 又∵ABCD与ABEF为正方形, ∴△CMT≌△MNH. ∴MT=NH. ∴四边形MNHT是平行四边形. ∴MN∥TH. 又∵HT平面BCE,MN ∴MN∥平面BCE. 证法二:如下图,连结AN并延长交BE于P点,连结CP,
∵BE∥AF, ∴AN∶NP=FN∶NB. 又∵AM=FN, ∴NB=MC. ∴AN∶NP=AM∶MC. ∴MN∥CP. ∵CP ∴MN∥平面CBE. 思路分析:要证MN∥平面CBE须找到平面BCE内与MN平行的“目标直线”. 温馨提示:(1)要证线面平行,即须证线线平行,即将空间问题转化为平面问题解决,这是数学上常用的化归思想. (2)由直线和平面平行的判定定理可以知道,证明直线和平面平行只需要在平面内找到一条直线和这条直线平行即可.有时平面内的这条直线是图形中原来就有的,而有时图形中却没有现成的直线和这条直线平行.这时问题的关键是如何在平面内寻求一条直线和该直线平行.例1中的证法一这种构造“目标直线的方法我们形象地称为”平行光源投影法,即用一束平行于AB的光线照射MN,MN在面BCE内的投影即为目标直线.例1中的证法二这种构造“目标直线”的方法,我们形象地称之为“点光源投影法”,即将点A看作光源,MN在平面BCE内的投影即为所寻找的目标直线. |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
一个几何体的三视图如下图所示,其中主视图与左视图是腰长为6的等腰直角三角形,俯视图是正方形。

(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:

A.![]() B.arccos
B.arccos![]() C.arctan
C.arctan![]() D.arcsin
D.arcsin![]()
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)用a、θ表示S1和S2;
(2)当a固定,θ变化时,求![]() 取最小值时的角θ.
取最小值时的角θ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com