
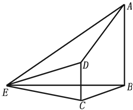
 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.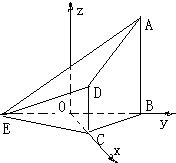 解法1:①取BE的中点O,连OC.
解法1:①取BE的中点O,连OC.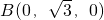 ,
,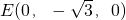 D(1,0,1),
D(1,0,1),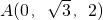 (4分)
(4分)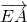 =
=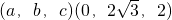 =
=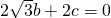 .
. =
=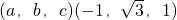 =
=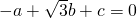 .
. =
=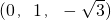 (6分)
(6分) =(1,0,0).
=(1,0,0). =
=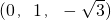 •(1,0,0)=0,
•(1,0,0)=0,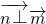
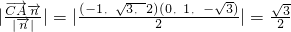 (12分)
(12分)
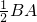
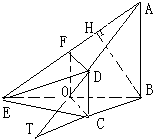

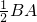 ,OF
,OF CD
CD
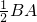 ,延长AD,BC交于T
,延长AD,BC交于T .(8分)
.(8分) ,AB=2,
,AB=2, ,
, (12分)
(12分)
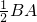 ,延长AD,BC交于T,得到C为BT的中点.得到点C到平面ADE的距离等于点B到平面ADE的距离的
,延长AD,BC交于T,得到C为BT的中点.得到点C到平面ADE的距离等于点B到平面ADE的距离的 ,做出结果.
,做出结果. .或取A B的中点M.易证CM∥DA.点C到平面ADE的距离等于点M到平面ADE的距离为
.或取A B的中点M.易证CM∥DA.点C到平面ADE的距离等于点M到平面ADE的距离为 .
. 

科目:高中数学 来源: 题型:
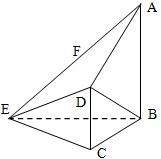 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.查看答案和解析>>
科目:高中数学 来源: 题型:
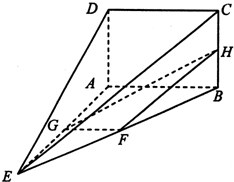 (2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点| GP |
| GF |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分) 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
AB=BC=CE=2CD=2,∠BCE=1200,F为AE中点。
(Ⅰ) 求证:平面ADE⊥平面ABE ;
(Ⅱ) 求二面角A—EB—D的大小的余弦值;
(Ⅲ)求点F到平面BDE的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com