
����Ŀ��ij��˾Ϊ�������״��������������1��������Ϊ5Ԫ/��������2����������Ϊ2Ԫ/��������ij��������Ӫ����������Ե㣨ÿ���Ե�����ֻ����һ�ִ����������������һ��Աȸõ�����һ��ȵ����������������Ӧ�ĵȸ�����ͼ��ͼ��ʾ�� 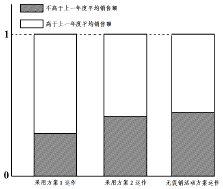
��1������ݵȸ�����ͼ�ṩ����Ϣ��Ϊ�ù�˾����ѡ��һ��Ϊ�����Ĵ��������������˵�����ɣ���
��2����֪�ù�˾��Ʒ�ijɱ�Ϊ10Ԫ/����δ����������������ã���Ϊ�ƶ�����ȸõ����IJ�Ʒ���ۼ۸�ͳ����һ��ȵ�8���ۼ�xi����λ��Ԫ/����������������yi����λ��������i=1��2������8�����±���ʾ��
�ۼ�x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
����y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
��������������ݼ�����Ӧ�����ָ��R2 �� �����ݼ�������ѡ����ʵĻع�ģ�ͽ�����ϣ�
�ڸ�����ѡ�ع�ģ�ͣ������ۼ�x��Ϊ����ʱ������z���Դﵽ���
| | | |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
���������ָ��  ��
��
���𰸡�
��1���⣺�ɵȸ�����ͼ��֪�����ƽ�����۶��뷽��1�����������ǿ�ڷ���2
��2���⣺������֪���ݿ�֪���ع�ģ�� ![]() ��Ӧ�����ָ��
��Ӧ�����ָ�� ![]() ��
��
�ع�ģ�� ![]() ��Ӧ�����ָ��
��Ӧ�����ָ�� ![]() ��
��
�ع�ģ�� ![]() ��Ӧ�����ָ��
��Ӧ�����ָ�� ![]() ��
��
��Ϊ ![]() �����Բ��ûع�ģ��
�����Բ��ûع�ģ�� ![]() ���������Ϊ���ʣ�
���������Ϊ���ʣ�
���ɣ�1����֪�����÷���1������Ч���Ϸ���2�ã�
�������� ![]() ��z'=����x+30����x��40����
��z'=����x+30����x��40����
��x�ʣ�0��40��ʱ�� ![]() ����������
����������
��x�ʣ�40��+�ޣ�ʱ�� ![]() �����ݼ���
�����ݼ���
�ʵ��ۼ�x=40ʱ������ﵽ���
����������1���ɵȸ�����ͼ��֪�����ƽ�����۶��뷽��1�����������ǿ�ڷ���2����2����������ָ�����ȽϿɵý��ۣ�
���ɣ�1����֪�����÷���1������Ч���Ϸ���2�ã��������� ![]() �����õ����ķ������ɵý��ۣ�
�����õ����ķ������ɵý��ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ʵ��x������ʽx2+a|x|+1��0���������ʵ��a��ȡֵ��Χ�ǣ� ��
A.�����ޣ���2��
B.[��2��+�ޣ�
C.[��2��2]
D.[0��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ���۾�˶�������ɫ�����������ž������С�����ˮ�������ݡ�֮��������ijˮ�ɻ����ʦ�ܹ�ÿ����250��ˮ�ɻ������ʦÿ���һ����1.2Ԫ��������ʦ���쳬������������IJ���ÿ��1.7Ԫ���������δ�ܰ������������ʵ����ɵĵ������ȡ���칤�ʣ� ��I������ʦ�������루��λ��Ԫ�����ڵ����n����λ������n��N���ĺ�������ʽf��n����
���õ��ʦ��¼�˹�ȥ10��ÿ��ĵ����n����λ�������������������
�����n | 210 | 230 | 250 | 270 | 300 |
Ƶ�� | 1 | 2 | 3 | 3 | 1 |
��10���¼�ĸ��������Ƶ����Ϊ������������ĸ��ʣ�
��������õ��ʦ��10���ƽ�����룻
��������õ��ʦ�������벻����300Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=��x��a����x��b����x��c��������a��1��b��1����x=0��f��x����һ����㣬����y=f��x���ڵ㣨1��f��1������������ƽ����x�ᣬ��a+b����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ִ����ͼ��ʾ�ij����ͼ���������k��b��r��ֵ�ֱ�Ϊ2��2��4�������i��ֵ�ǣ� �� 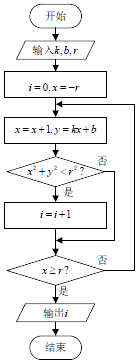
A.4
B.3
C.6
D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��쳲���������{an}���㣺 ![]() ���������е�ÿһ�����ͼ�����Ž������ÿһС���ӵı߳�Ϊ1����ǰn����ռ�ĸ��ӵ����֮��ΪSn �� ÿ���������������ڵ���������Χ�ɵ��������Ϊcn �� �����н��۴�����ǣ� ��
���������е�ÿһ�����ͼ�����Ž������ÿһС���ӵı߳�Ϊ1����ǰn����ռ�ĸ��ӵ����֮��ΪSn �� ÿ���������������ڵ���������Χ�ɵ��������Ϊcn �� �����н��۴�����ǣ� �� 
A.![]()
B.a1+a2+a3+��+an=an+2��1
C.a1+a3+a5+��+a2n��1=a2n��1
D.4��cn��cn��1��=��an��2an+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ���ڵ�������ABCD�У� ![]() ���ѡ�ABE��BE����ʹ��
���ѡ�ABE��BE����ʹ�� ![]() ���õ�����A��BCDE����ͼ2��ʾ��
���õ�����A��BCDE����ͼ2��ʾ�� 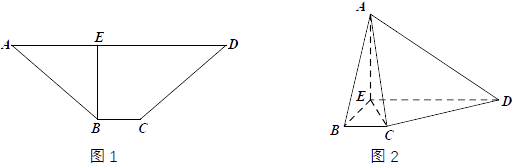
��1����֤����ACE����ABD��
��2����ƽ��ABE��ƽ��ACD���������ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin2xcos ![]() �� ��������f��x������С�����ںͶԳ���ķ��̣�
�� ��������f��x������С�����ںͶԳ���ķ��̣�
��������f��x�������� ![]() �ϵ����ֵ��
�ϵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() =��
=�� ![]() sin��x��1����
sin��x��1���� ![]() =��cos��x��cos2��x+1�����躯��f��x��=
=��cos��x��cos2��x+1�����躯��f��x��= ![]() ��
��
��1��������f��x����ͼ�����ֱ��x= ![]() �Գƣ��Ҧء�[0��3]ʱ������f��x���ĵ��������䣻
�Գƣ��Ҧء�[0��3]ʱ������f��x���ĵ��������䣻
��2���ڣ�1���������£��� ![]() ʱ������f��x������ֻ��һ����㣬��ʵ��b��ȡֵ��Χ��
ʱ������f��x������ֻ��һ����㣬��ʵ��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com