
【题目】如图,∠C= ![]() ,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为
,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为 ![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( ) 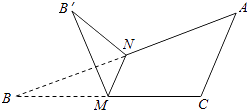
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵∠C= ![]() ,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为
,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为 ![]() ,
,
∴∠BMB′= ![]() ,
,
取BM的中点D,连B′D,ND,
由于折叠之前BM与CM都始终垂直于MN,这在折叠之后仍然成立,
∴折叠之后平面B′MN与平面BMN所成的二面角即为∠B′MD=60°,
并且B′在底面ACB内的投影点D就在BC上,且恰在BM的中点位置,
∴B′D⊥BC,B′D⊥AD,B′D⊥面ABC,
∴∠B′ND就为斜线B′N与平面ABC所成的角
设AC=BC=a,则B′D= ![]() ,B′N=
,B′N= ![]() ,DN=
,DN= ![]()
![]() ,
,
tan∠B′ND= ![]() =
= ![]() =
= ![]() .
.
故B'N与平面ABC所成角的正切值是 ![]() .
.
故选:D.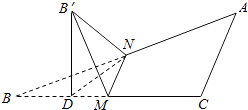
【考点精析】认真审题,首先需要了解空间角的异面直线所成的角(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则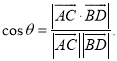 ).
).


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y关于t的回归方程 ![]() =
= ![]() t+
t+ ![]() .
.
(Ⅱ)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
附:回归方程 ![]() =
= ![]() t+
t+ ![]() 中
中 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移 ![]() 个单位,沿y轴向下平移1个单位,得到函数y=
个单位,沿y轴向下平移1个单位,得到函数y= ![]() sinx的图象,则y=f(x)的解析式为( )
sinx的图象,则y=f(x)的解析式为( )
A.y= ![]() sin(2x+
sin(2x+ ![]() )+1
)+1
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1
)+1
C.y= ![]() sin(
sin( ![]() x+
x+ ![]() )+1
)+1
D.y= ![]() sin(
sin( ![]() x﹣
x﹣ ![]() )+1
)+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Sn为等差数列{an}的前n项和,且a1=1,S7=28,记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1. (Ⅰ)求b1 , b11 , b101;
(Ⅱ)求数列{bn}的前1000项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx,将函数y=f(x)的图象向右平移![]() 个单位,再把横坐标缩短到原来的
个单位,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的解析式,并写出它的单调递增区间.
(纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的解析式,并写出它的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将A,B两枚骰子各抛掷一次,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)两枚骰子点数之和是3的倍数的结果有多少种?
(3)两枚骰子点数之和是3的倍数的概率为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD= ![]() ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点.
(Ⅰ)证明:平面EAC⊥平面PBD;
(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.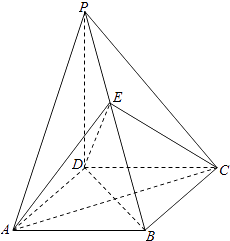
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中,正确的是( )
A.幂函数的图象都通过点(0,0),(1,1)
B.幂函数的图象可以出现在第四象限
C.当幂指数α取1,3, ![]() 时,幂函数y=xα是增函数
时,幂函数y=xα是增函数
D.当幂指数α=-1时,幂函数y=xα在定义域上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三内角A、B、C成等差数列,sinA、sinB、sinC成等比数列,则这个三角形的形状是( )
A.直角三角形
B.钝角三角形
C.等腰直角三角形
D.等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com