
已知函数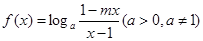 的图象关于原点对称。
的图象关于原点对称。
(1)求m的值;(2)判断 在
在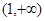 上的单调性,并根据定义证明。
上的单调性,并根据定义证明。
(1) ;(2)当
;(2)当 时,
时, ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调增;当
上单调增;当 时,
时,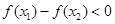 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调减。
上单调减。
【解析】
试题分析:(1)由已知条件得 ------------2分
------------2分
即 ,
, ,即
,即 ------2分
------2分
当 时,
时, 无意义,故
无意义,故 舍去
舍去
因此,只有 满足题意-----------2分
满足题意-----------2分
(2)由(1)知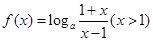 ,设
,设
则
 ,且
,且 ,
, ,
, ------------4分
------------4分
当 时,
时, ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调增
上单调增
当 时,
时,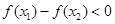 ,由函数单调性定义知
,由函数单调性定义知 在
在 上单调减
上单调减
-----------------3分
考点:函数的奇偶性;函数的单调性;用定义法证明函数的单调性。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。


科目:高中数学 来源: 题型:022
(
山东胜利一中模拟)已知下列命题:A.![]() ;
;
B.函数f(|x|-1)的图象向左平移1个单位后得到的函数图象解析式为y=f(|x|);
C.函数y=f(1+x)的图象与函数y=f(1-x)的图象关于y轴对称;
D.满足条件 ,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来)
,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来)
查看答案和解析>>
科目:高中数学 来源: 题型:022
(2006
北京东城模拟)已知函数 ,给出下列命题:
,给出下列命题:
A.f(x)不可能为偶函数;
B.当f(0)=f(2)时,f(x)的图象必关于直线x=1对称;
C.若 ,则f(x)在区间[a,+∞)上是增函数;
,则f(x)在区间[a,+∞)上是增函数;
D.f(x)
有最小值 ,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).
,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com