
在如图的三棱锥P—ABC中,PA⊥平面ABC,PA=AC=1,PC= BC,PB和平面ABC所成的角为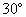 .
.
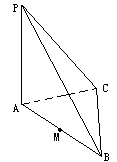
(Ⅰ)求证:平面PBC⊥平面PAC;
(Ⅱ)比较三个侧面的面积的算术平均数与底面积数值的大小,并说明理由;
(Ⅲ)求AB的中点M到直线PC的距离.
|
解:(Ⅰ)由已知PA⊥平面ABC,PA=AC=1, ∴△PAC为等腰直角三角形,且PC=CB= 在Rt△PAB中∠PBA= ∴PB=2, ∴△PCB为等腰直角三角形. ∵PA⊥平面ABC,PC⊥BC, ∴AC⊥BC,又AC∩PC=C, ∴BC⊥平面PAC, ∵BC ∴平面PBC⊥平面PAC (Ⅱ)三个侧面及底面都是直角三角形,求得侧面PAC面积值为 三个侧面面积的算术平均数为 ∴三个侧面面积的算术平均数大于底面积的数值. (Ⅲ)如图,过M作MD⊥AC,垂足为D
∵平面PAC⊥平面ABC且相交于AC, ∴MD⊥平面PAC. 过D作DE⊥PC,垂足为E,连结ME,则DE是ME在平面PBC上的射影, ∵DE⊥PC,∴ME⊥PC,ME的长度即是M到PC的距离. 在Rt△ABC中,MD∥BC,MD= DE=DCsin ∴ME= |


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
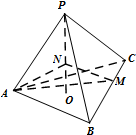 如图,三棱锥P-ABC的高PO=8,AC=BC=3,∠ACB=30°,M、N分别在BC和PO上,且CM=x,PN=2CM,则下面四个图象中大致描绘了三棱锥N-AMC的体积V与x变化关系(x∈(0,3])( )
如图,三棱锥P-ABC的高PO=8,AC=BC=3,∠ACB=30°,M、N分别在BC和PO上,且CM=x,PN=2CM,则下面四个图象中大致描绘了三棱锥N-AMC的体积V与x变化关系(x∈(0,3])( )A、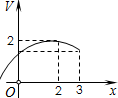 | B、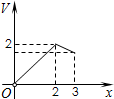 | C、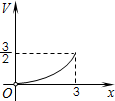 | D、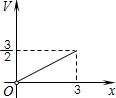 |
查看答案和解析>>
科目:高中数学 来源: 题型:
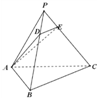 如图,三棱锥P-ABC的底面是正三角形,各条侧棱均相等,∠APB<60°.设点D、E分别在线段PB、PC上,且DE∥BC,记PD=x,△ADE周长为y,则y=f(x)的图象可能是( )
如图,三棱锥P-ABC的底面是正三角形,各条侧棱均相等,∠APB<60°.设点D、E分别在线段PB、PC上,且DE∥BC,记PD=x,△ADE周长为y,则y=f(x)的图象可能是( )查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.查看答案和解析>>
科目:高中数学 来源: 题型:
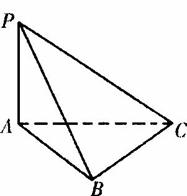
A.4π B.37π C.27π D.π
查看答案和解析>>
科目:高中数学 来源: 题型:
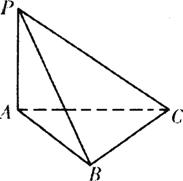
A.4π B.3π C.2π D.π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com