
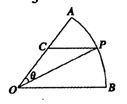
如图所示,扇形AOB,圆心角AOB的大小等于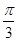 ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
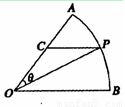
(1)若C是半径OA的中点,求线段PC的长;
(2)设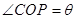 ,求
,求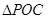 面积的最大值及此时
面积的最大值及此时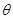 的值.
的值.
(1)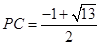 ;(2)
;(2)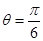 时,
时,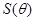 取得最大值为
取得最大值为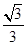 .
.
【解析】
试题分析:本题考查解三角形中正弦定理、余弦定理的应用,三角形面积公式以及运用三角公式进行恒等变形,考查学生的分析能力和计算能力.第一问,在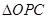 中,
中,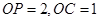 ,
,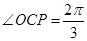 ,由余弦定理求边长
,由余弦定理求边长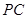 ;第二问,在
;第二问,在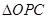 中,利用正弦定理,得到
中,利用正弦定理,得到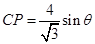 ,
,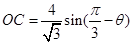 ,三角形面积公式
,三角形面积公式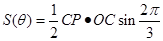 ,将上面2个边长代入,利用二倍角公式、降幂公式、两角和与差的正弦公式化简表达式,再求三角函数的最值.
,将上面2个边长代入,利用二倍角公式、降幂公式、两角和与差的正弦公式化简表达式,再求三角函数的最值.
试题解析:(1)在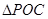 中,
中,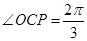 ,
,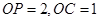 ,由
,由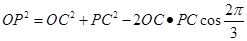 ,
,
得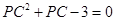 ,解得
,解得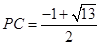 .
.
(2)∵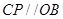 ,∴
,∴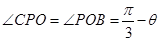 ,
,
在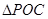 中,由正弦定理得
中,由正弦定理得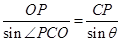 ,即
,即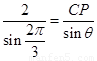 ,
,
∴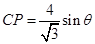 ,又
,又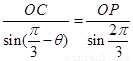 ,
,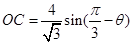 .
.
记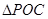 的面积为
的面积为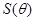 ,则
,则
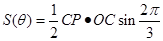
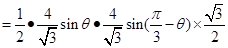
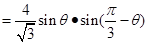
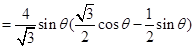
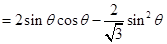
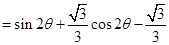
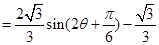
∴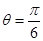 时,
时,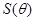 取得最大值为
取得最大值为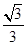 .
.
考点:1.余弦定理;2.正弦定理;3.二倍角公式;4.降幂公式;5.两角和与差的正弦公式.


科目:高中数学 来源: 题型:
 (2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于
(2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于
(2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=![]() ,求△POC面积的最大值及此时
,求△POC面积的最大值及此时![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=![]() ,求△POC面积的最大值及此时
,求△POC面积的最大值及此时![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com