
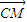 +
+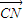 |=|
|=|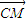 -
-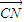 |,求l的方程.
|,求l的方程.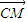 +
+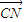 |=|
|=|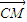 -
-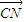 |,可得
|,可得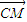 •
•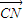 =0,设M(x1,y1),N(x2,y2),可得x1x2-(x1+x2)+1+y1y2=0,分类讨论:①直线l的斜率存在时,设直线方程为y=k(x+1)代入椭圆方程,整理利用韦达定理,可求k的值,从而可得直线的方程;②当直线l的斜率不存在时,l的方程为x=-1,M(-1,
=0,设M(x1,y1),N(x2,y2),可得x1x2-(x1+x2)+1+y1y2=0,分类讨论:①直线l的斜率存在时,设直线方程为y=k(x+1)代入椭圆方程,整理利用韦达定理,可求k的值,从而可得直线的方程;②当直线l的斜率不存在时,l的方程为x=-1,M(-1, ),N(-1,-
),N(-1,- ),
),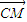 •
•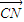 ≠0,从而可得结论.
≠0,从而可得结论. 得b+c=4,即|AC|+|AB|=4(定值).
得b+c=4,即|AC|+|AB|=4(定值). .
.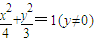 . …(4分)
. …(4分)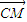 +
+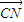 |=|
|=|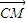 -
-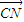 |,
|,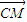 +
+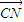 |2=|
|2=| -
-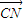 |2,展开得
|2,展开得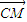 •
•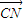 =0,
=0,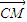 =(x1-1,y1),
=(x1-1,y1),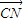 =(x2-1,y2),
=(x2-1,y2),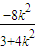 ,x1x2=
,x1x2= .
.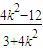 +(k2-1)×
+(k2-1)×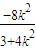 +k2+1=0,
+k2+1=0,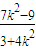 =0,解得k=±
=0,解得k=±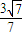 .
. x+
x+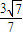 ,或y=-
,或y=-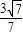 x-
x-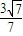 .…(10分)
.…(10分) ),N(-1,-
),N(-1,- ),
),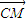 •
•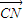 =(-2,
=(-2, )•(-2,-
)•(-2,- )=4-3=1≠0,∴不满足题意.
)=4-3=1≠0,∴不满足题意.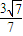 x+
x+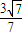 ,或y=-
,或y=-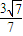 x-
x-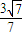 .…(12分)
.…(12分)

 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
| CM |
| CN |
| CM |
| CN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南郑州高三第一次质量预测理数学试卷(解析版) 题型:解答题
在△ABC中,顶点A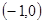 ,B
,B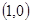 ,动点D,E满足:①
,动点D,E满足:①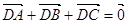 ;②
;②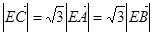 ,③
,③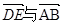 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)是否存在圆心在原点的圆,只要该圆的切线与顶点C的轨迹有两个不同交点M,N,就一定有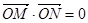 ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南郑州高三第一次质量预测文科数学试卷(解析版) 题型:解答题
在△ABC中,顶点A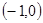 ,B
,B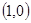 ,动点D,E满足:①
,动点D,E满足:①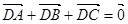 ;②
;②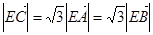 ,③
,③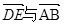 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)若斜率为1直线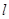 与动点C的轨迹交与M,N两点,且
与动点C的轨迹交与M,N两点,且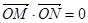 ,求直线
,求直线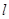 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省镇平一高高三下学期第四次周考文科数学试卷 题型:解答题
.(本小题满分12分)
在△ABC中,顶点A(-1,0),B(1,0),动点D,E满足:
①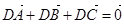 ;②|
;②|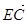 |=
|=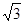 |
|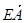 |=
|=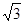 |
|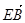 |③
|③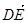 与
与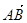 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)
若斜率为1直线l与动点C的轨迹交于M,N两点,且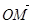 ·
·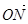 =0,求直线l的方程.
=0,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com