
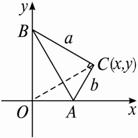
思路分析:由已知∠ACB是直角,A和B两点在坐标轴上滑动时,∠AOB也是直角,由平面几何知识,A、C、B、O四点共圆,则有∠ABC=∠AOC,这就是点C满足的几何条件.
由此列出顶点C的坐标适合的方程.

解:设点C的坐标为(x,y),连结CO,
由∠ACB=∠AOB=90°,所以A、O、B、C四点共圆.
从而∠AOC=∠ABC.由tan∠ABC=![]() ,tan∠AOC=
,tan∠AOC=![]() ,有
,有![]() 即y=
即y=![]() x,
x,
(注意到方程表示的是过原点、斜率为![]() 的一条直线,而题目中的A与B均在两坐标轴的正半轴上滑动,由于a、b为常数,故C点的轨迹不会是一条直线,而是直线的一部分.我们可考察A与B两点在坐标轴上的极端位置,确定C点坐标的范围)
的一条直线,而题目中的A与B均在两坐标轴的正半轴上滑动,由于a、b为常数,故C点的轨迹不会是一条直线,而是直线的一部分.我们可考察A与B两点在坐标轴上的极端位置,确定C点坐标的范围)
如图,当点A与原点重合时,
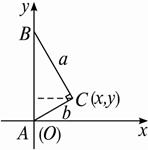
S△ABC=![]() ·x=
·x=![]() ·x,所以x=
·x,所以x=![]() .
.
如图,当点B与原点重合时,C点的横坐标x=BD.
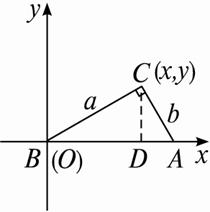
由射影定理,BC2=BD·AB,,即
a2=x·![]() ,
,
有x=![]() .由已知a>b,所以
.由已知a>b,所以![]() .
.
故C点的轨迹方程为y=![]() (
(![]() ).
).


科目:高中数学 来源: 题型:
 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-2
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,- ),顶点C在x轴上.
),顶点C在x轴上.查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京四中高二(上)期中数学试卷(解析版) 题型:解答题
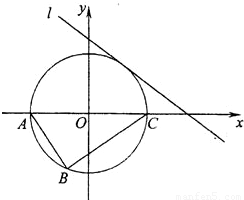 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-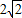 ),顶点C在x轴上.
),顶点C在x轴上.查看答案和解析>>
科目:高中数学 来源:2007-2008学年北京四中高一(下)期末数学试卷(解析版) 题型:解答题
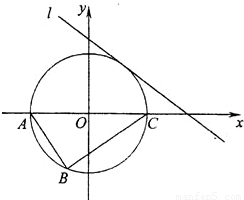 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-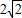 ),顶点C在x轴上.
),顶点C在x轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com