
已知三角形的三个顶点是A(4,0),B(6,6),C(0,2).
(1)求AB边上的高所在直线的方程;
(2)求AC边上的中线所在直线的方程.
(1)x+3y﹣6=0;(2)5x﹣4y﹣5=0.
【解析】
试题分析:
解题思路:(1)因为AB边上的高所在直线经过点C(0,2),且与AB垂直,所以先求出AB的斜率,再根据垂直求出CD的斜率,然后写出直线的点斜式方程,化成一般式即可;(2)因为AC边上的中线所在直线经过点B与CD 的中点,所以先求出CD的中点坐标,写出直线的两点式方程,化成一般式即可.
规律总结:求直线方程,要根据题意恰当地设出直线方程的形式(点斜式、斜截式、两点式、截距式、一般式),再利用直线间的位置关系(平行、垂直、相交)进行求解.
试题解析:(1)∵A(4,0),B(6,6),C(0,2),∴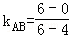 =3,
=3,
∴AB边上的高所在直线的斜率k=﹣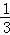 ,
,
∴AB边上的高所在直线的方程为y﹣2=﹣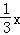 ,整理,得x+3y﹣6=0.
,整理,得x+3y﹣6=0.
(2)∵AC边的中点为(2,1),
∴AC边上的中线所在的直线方程为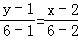 ,
,
整理,得5x﹣4y﹣5=0.
考点:1.直线方程;2.中点坐标公式;3.两直线间的位置关系.


科目:高中数学 来源:2016届山西省高一下学期期中考试数学试卷(解析版) 题型:选择题
在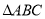 中,若
中,若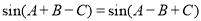 ,则
,则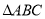 必是( )
必是( )
A.等腰三角形 B.直角三角形
C.等腰或直角三角形 D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源:2016届山东省滨州市高一下学期期末考试数学试卷(解析版) 题型:解答题
已知单调递增的等比数列{an}满足a1+a2+a3=14,且a2+1是a1,a3的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=anlog2an,求数列{bn}的前n项和Sn;
(3)若存在n∈N*,使得Sn+1﹣2≤8n3λ成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源:2016届山东省滨州市高一下学期期末考试数学试卷(解析版) 题型:选择题
在等差数列{an}中,若a3+a7=10,则等差数列{an}的前9项和S9等于( ).
A.45 B.48 C.54 D.108
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一二月检测数学试卷(解析版) 题型:解答题
若点M是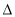 ABC所在平面内一点,且满足:
ABC所在平面内一点,且满足: .
.
(1)求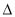 ABM与
ABM与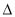 ABC的面积之比.
ABC的面积之比.
(2)若N为AB中点,AM与CN交于点O,设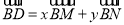 ,求
,求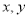 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com