Question

设有长方体ABCD－A′B′C′D′如图所示，长、宽、高分别为|AB|＝4 cm，|AD|＝3 cm，|AA′|＝5 cm，N是线段CC′的中点．分别以AB，AD，AA′所在的直线为x轴、y轴、z轴，以1 cm为单位长，建立空间直角坐标系．

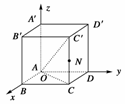
(1)求A、B、C、D、A′、B′、C′、D′的坐标；

(2)求N的坐标．

Answer 1

　(1)A，B，C，D都在平面xOy内，点的竖坐标都为0，它们在x轴、y轴所组成的直角坐标系中的坐标分别是(0,0)、(4,0)、(4,3)、(0,3)，因此空间坐标分别是A(0,0,0)、B(4,0,0)、C(4,3,0)、D(0,3,0)．

A′、B′、C′、D′同在一个垂直于z轴的平面内，这个平面与z轴的交点A′在z轴上的坐标是5，故这四点的z的坐标都是5.从这四点作xOy平面的垂线交xOy平面于A、B、C、D四点，故A′、B′、C′、D′的x，y坐标分别与A、B、C、D相同，由此可知它们的空间坐标分别是A′(0,0,5)、B′(4,0,5)、C′(4,3,5)、D′(0,3,5)．

(2)N是线段CC′的中点，有向线段CN的方向与z轴正方向相同，|CN|＝2.5，因此N的z坐标为2.5，C在xOy平面内的平面坐标为(4,3)，这就是N的x、y坐标，故N的空间坐标为(4,3,2.5)．