
已知 的图象关于坐标原点对称。
的图象关于坐标原点对称。
(1)求 的值,并求出函数
的值,并求出函数 的零点;
的零点;
(2)若函数 在[0,1]内存在零点,求实数b的取值范围;
在[0,1]内存在零点,求实数b的取值范围;
(3)设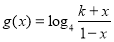 ,已知
,已知 的反函数
的反函数 =
= ,若不等式
,若不等式 在
在 上恒成立,求满足条件的最小整数k的值。
上恒成立,求满足条件的最小整数k的值。
(1)F(x)的零点为x=1;(2)2≤b≤7;(3)满足条件的最小整数k的值是8
【解析】
试题分析:(1)根据函数的图象关于原点对称,可得f(x)是定义在R的奇函数,图象必过原点,即f(0)=0,求出a的值,求出函数F(x)的解析式,解指数方程求求出函数的零点;
(2)函数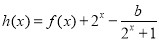 在[0,1]内存在零点,方程(2x)2+2x+1-1-b=0在[0,1]内有解,分析函数b=(2x)2+2x+1-1在[0,1]内的单调性,及端点的函数值符号,进而根据零点存在定理得到结论;
在[0,1]内存在零点,方程(2x)2+2x+1-1-b=0在[0,1]内有解,分析函数b=(2x)2+2x+1-1在[0,1]内的单调性,及端点的函数值符号,进而根据零点存在定理得到结论;
(3)由不等式f-1(x)≤g(x)在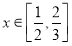 上恒成立,利用基本不等式可求出满足条件的k的范围,进而求出最小整数k的值.
上恒成立,利用基本不等式可求出满足条件的k的范围,进而求出最小整数k的值.
试题解析:(1)由题意知f(x)是R上的奇函数,

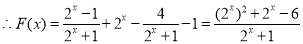
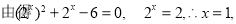
即F(x)的零点为x=1. 4分
(2)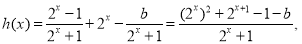
由题设知h(x)=0在[0,1]内有解,
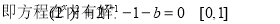
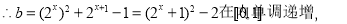
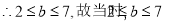
 在[0,1]内存在零点 8分
在[0,1]内存在零点 8分
(3)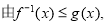
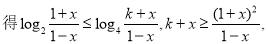
显然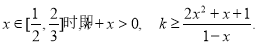
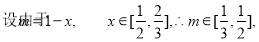

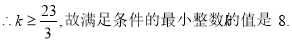 14分
14分
考点:函数的性质的综合应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016届河南周口市英文学校高一上学期第三次月考数学试卷(解析版) 题型:选择题
已知正方体的外接球的体积是 ,则这个正方体的棱长是( )
,则这个正方体的棱长是( )
A. B.
B. C.
C.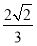 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届河北省邯郸市高一上学期期末考试数学试卷(解析版) 题型:选择题
已知函数 ,若关于
,若关于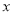 的方程
的方程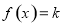 有两个不同的根,则实数
有两个不同的根,则实数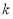 的取值范围是( )
的取值范围是( )
A.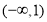 B.
B.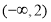 C.
C. D.
D.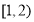
查看答案和解析>>
科目:高中数学 来源:2016届江西鹰潭市高一上学期期末考试理科数学试卷(解析版) 题型:选择题
函数f(x)的定义域为D,满足:①f(x)在D内是单调函数;②存在[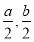 ]
]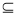 D,使得f(x)在[
D,使得f(x)在[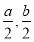 ]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx-t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx-t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
A. (0,1) B. (0,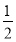 ) C. (-∞,
) C. (-∞,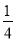 ) D. (0,
) D. (0,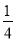 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com