
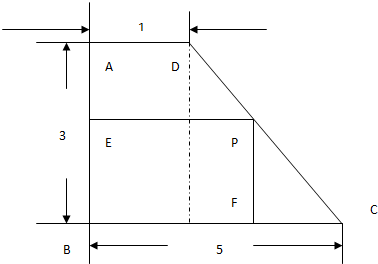
 有一块形状为直角梯形材料ABCD,其尺寸如图所示(单位:分米),现从中截取一块矩形材料EBFP,点P在CD上,设FP=x
有一块形状为直角梯形材料ABCD,其尺寸如图所示(单位:分米),现从中截取一块矩形材料EBFP,点P在CD上,设FP=x 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
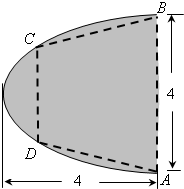 如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的对称轴对称且AB=4,抛物线的顶点到底边AB的距离是4,记CD=2t,梯形面积为S.以抛物线的顶点为坐标原点,其对称轴为x轴,建立平面直角坐标系.
如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的对称轴对称且AB=4,抛物线的顶点到底边AB的距离是4,记CD=2t,梯形面积为S.以抛物线的顶点为坐标原点,其对称轴为x轴,建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:
 有一块形状为直角梯形材料ABCD,其尺寸如图所示(单位:分米),现从中截取一块矩形材料EBFP,点P在CD上,设FP=x
有一块形状为直角梯形材料ABCD,其尺寸如图所示(单位:分米),现从中截取一块矩形材料EBFP,点P在CD上,设FP=x查看答案和解析>>
科目:高中数学 来源: 题型:
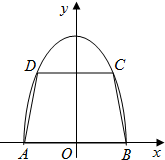 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.以AB为x轴,AB中点为原点建立平面直角坐标系.
如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.以AB为x轴,AB中点为原点建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市高二(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com