
一条动直线中,待定系数
t取不同的值,将得到不同的直线,所有这此直线构成一簇直线系,试问这些直线是不是一定通过某一定点呢?试就下列诸直线系分别进行讨论.(1)l
:x+ty=t-1;(2)l:tx+(t+1)y=1;
(3)l:x+2y+3+l (3x+4y+10)=0;
(4)l:x+y+t=0;
(5)l: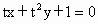
|
解: (1)令y=1,得x=-1,即动直线l过定点P(-1,1).(2) 令t=0,得直线y=1;令t=-1,得直线x=-1,则得点 P(-1,1),经检验,它满足原动直线的方程,故点P(-1,1)是动直线l所经过的定点.(3) 令l =0得x+2y+3=0,令l =-1,得2x+2y+7=0.解上述两个方程所组成的方程组,得 
将点 P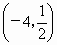 代入原动直线的方程中,有 代入原动直线的方程中,有
- 4+1+3l (-12+2+10)=0,∴ 点P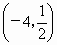 是直线l所经过的定点. 是直线l所经过的定点.
(4) 令t=0,得x+y=0,令t=1,得x+y=-1.易知上述两个方程组所组成的方程组无实数解. ∴ 该动直线不经过某一定点.(5) 令t=1,得x+y+1=0,令t=-1,得-x+y+1=0.解由上述两个方程所组成的方程组,得 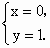
代入原直线方程中,得 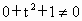 ,∴原动直线不经过定点. ,∴原动直线不经过定点. |


科目:高中数学 来源:数学教研室 题型:044
一条动直线中,待定系数t取不同的值,将得到不同的直线,所有这此直线构成一簇直线系,试问这些直线是不是一定通过某一定点呢?试就下列诸直线系分别进行讨论.
(1)l:x+ty=t-1;(2)l:tx+(t+1)y=1;(3)l:x+2y+3+l
(3x+4y+10)=0;(4)l:x+y+t=0;(5)l: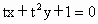
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com