
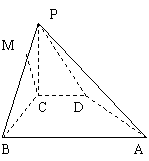
(满分12分)如图所示,在四棱锥P-ABCD中,![]() 平面ABCD,PC=2,在四边形ABCD中,
平面ABCD,PC=2,在四边形ABCD中,![]() ,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成
,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成![]() 的角.
的角.
(1)求证:![]() // 平面PAD;
// 平面PAD;
(2)点C到平面PAD的距离.
 |
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:2012-2013学年黑龙江省高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图所示,在直棱柱 中,
中, ,
,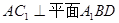 ,
, 的中点.
的中点.

(1)求证: ∥
∥ ;
;
(2)求证: ;
;
(3)在 上是否存在一点
上是否存在一点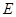 ,使得
,使得 ,若存在,试确定
,若存在,试确定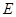 的位置,并判断
的位置,并判断 与平面
与平面 是否垂直?若不存在,请说明理由.
是否垂直?若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届云南省芒市高二下期末数学试卷(解析版) 题型:解答题
(本题满分12分)
如图所示,已知 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC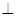 CD.
CD.
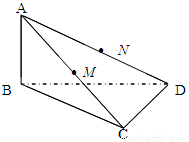
(Ⅰ)求证:MN∥平面BCD;
(Ⅱ)求证:平面B CD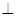 平面ABC;
平面ABC;
(Ⅲ)若AB=1,BC=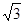 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省南昌市高三第六次月考数学理卷 题型:解答题
(本题满分12分)如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
 (1)求证:PO⊥面ABCE;
(1)求证:PO⊥面ABCE;
(2)求AC与面PAB所成角 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源:2010年河北省邯郸市高三第二次数学文科试题 题型:解答题
(本小题满分12分)
如图所示,在正三棱柱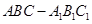 中,底面边长为
中,底面边长为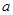 ,侧棱长为
,侧棱长为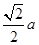 ,
,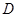 是棱
是棱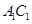 的中点.
的中点.
|
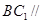 平面
平面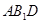 ;
;
(Ⅱ)求二面角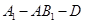 的大小;[来源:ZXXK]
的大小;[来源:ZXXK]
(Ⅲ)求点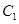 到平面
到平面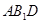 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2010-2011年河南省郑州市高二下学期第一次月考数学文卷 题型:解答题
(本小题满分12分)
如图所示茎叶图是青年歌手电视大奖赛中7位评委给参加最后决赛的两位选手甲、乙评定的成绩,程序框图用来编写程序统计每位选手的成绩(各评委所给有效分数的平均值),试根据下面条件回答下列问题:
1)根据茎叶图,乙选手的成绩中,中位数是 ,众数是 。
2)在程序框图中,用k表示评委人数,用a表示选手的最后成绩(各评委所给有效分数的平均值)那么图中①②处分别为 , 。“S1=S-max-min”的含义
” 。
3) 根据程序框图,甲的最后成绩是 ;乙的最后成绩是 。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com