
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,
且BC AE=DC
AE=DC AF,B、E、F、C四点共圆.
AF,B、E、F、C四点共圆.

(Ⅰ)证明:CA是△ABC外接圆的直径;
(Ⅱ)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.
(Ⅰ)见解析(Ⅱ)
【解析】(Ⅰ)因为CD为△ABC外接圆的切线,
所以 ,由题设知
,由题设知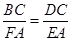 ,
,
故 ∽
∽ ,所以
,所以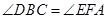 ,因为B、E、F、C四点共圆,所以
,因为B、E、F、C四点共圆,所以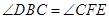 ,
,
故 ,所以
,所以 ,因此CA是△ABC外接圆的直径.
,因此CA是△ABC外接圆的直径.
(Ⅱ)设DB=BE=EA=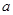 ,则由切割线定理可得:
,则由切割线定理可得:
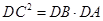 ,解得
,解得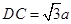 ,由(1)知:CA是△ABC外接圆的直径,所以
,由(1)知:CA是△ABC外接圆的直径,所以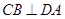 ,AC⊥CD,解得AC=
,AC⊥CD,解得AC=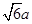 ,CE=
,CE=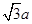 ,所以过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值为
,所以过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值为 =
= .
.
本题第(Ⅰ)问,由两个三角形相似可得出角相等,再由四点共圆,得出 ,从而得证;第(Ⅱ)问,由切割线定理以及B、E、F、C四点共圆,可以得出两圆的半径,从而得出面积的比值.对第(Ⅰ)问,不容易找到这两个三角形相似;第(Ⅱ)问中两个圆半径的求出容易出错.
,从而得证;第(Ⅱ)问,由切割线定理以及B、E、F、C四点共圆,可以得出两圆的半径,从而得出面积的比值.对第(Ⅰ)问,不容易找到这两个三角形相似;第(Ⅱ)问中两个圆半径的求出容易出错.
【考点定位】本小题主要考查圆的切线、割线、圆内接四边形、勾股定理等平面几何知识,考查数形结合思想,考查分析问题、解决问题的能力.


科目:高中数学 来源: 题型:
 【选修4-1几何证明选讲】
【选修4-1几何证明选讲】查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试文科数学(新课标2卷解析版) 题型:解答题
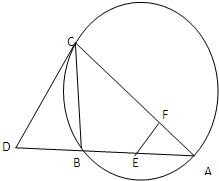
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D, E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B, E, F,C四点共圆。

证明:(Ⅰ)CA是△ABC外接圆的直径;
(Ⅱ)若DB=BE=EA.求过B, E, F,C四点的圆的面积与△ABC外接圆面积的比值.
查看答案和解析>>
科目:高中数学 来源:2013年全国统一高考数学试卷(文科)(新课标Ⅱ)(解析版) 题型:解答题
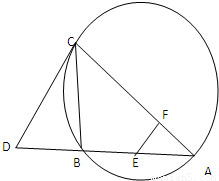 【选修4-1几何证明选讲】
【选修4-1几何证明选讲】查看答案和解析>>
科目:高中数学 来源:2013年全国统一高考数学试卷(理科)(新课标Ⅱ)(解析版) 题型:解答题
 【选修4-1几何证明选讲】
【选修4-1几何证明选讲】查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com