
(本题满分15分)如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.

(Ⅰ)求证:平面CBE⊥平面CDE;
(Ⅱ)求二面角C—BE—F的余弦值.
科目:高中数学 来源:2016届浙江省高三期中文科数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,已知抛物线
中,已知抛物线 的准线方程为
的准线方程为 ,过点
,过点 作抛物线的切线
作抛物线的切线 ,切点为
,切点为 (异于点
(异于点 ),直线
),直线 过点
过点 与抛物线交于两点
与抛物线交于两点 ,
, ,与直线
,与直线 交于点
交于点 .
.

(1)求抛物线的方程;
(2)试问: 的值是否为定值?若是,求出定值;若不是,说明理由.
的值是否为定值?若是,求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数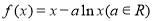 .
.
(1)当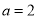 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)设函数 ,求函数
,求函数 的单调区间.
的单调区间.
【答案】(1) ;(2)当
;(2)当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增;当
上单调递增;当 时,
时, 在
在 上单调递增.
上单调递增.
【解析】
试题分析:(1)先求出切点,再利用导数的几何意义即可求出切线的斜率 ,从而问题解决;(2)先求出导函数
,从而问题解决;(2)先求出导函数 ,根据
,根据 求得的区间是单调增区间,
求得的区间是单调增区间,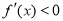 求得的区间是单调减区间,因为在函数式中含字母系数
求得的区间是单调减区间,因为在函数式中含字母系数 ,要对
,要对 分类讨论.
分类讨论.
试题解析:(1)当 时,
时, ,
, ,切点
,切点 ,
,
∴ ,∴
,∴ ,
,
∴曲线 在点
在点 处的切线方程为:
处的切线方程为: ,即
,即 .
.
(2) ,定义域为
,定义域为 ,
,
 ,
,
①当 ,即
,即 时,令
时,令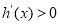 ,
,
∵ ,∴
,∴ ,
,
令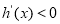 ,∵
,∵ ,∴
,∴ .
.
②当 ,即
,即 时,
时, 恒成立,
恒成立,
综上:当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
当 时,
时, 在
在 上单调递增.
上单调递增.
考点:1、导数的几何意义;2、利用导数研究函数的单调性.
【思路点睛】利用导数研究函数性质是导数的重要应用,一般是先求函数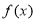 的定义域,利用不等式
的定义域,利用不等式 的解集与定义域的交集为函数的单调递增区间,
的解集与定义域的交集为函数的单调递增区间, 的解集与定义域的交集为函数的单调递减区间;若已知函数在某区间
的解集与定义域的交集为函数的单调递减区间;若已知函数在某区间 上单调递增(减),则转化为不等式
上单调递增(减),则转化为不等式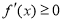 (
( )在区间
)在区间 上有解.
上有解.
【题型】解答题
【适用】一般
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分12分)已知椭圆E的两个焦点分别为 和
和 ,离心率
,离心率 .
.
(1)求椭圆E的方程;
(2)设直线 与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期期中理科数学试卷(解析版) 题型:解答题
(本小题满分10分)已知集合 .
.
(1)若 ,求出实数
,求出实数 的值;
的值;
(2)若命题 命题
命题 且
且 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数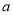 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届吉林省高三上学期二模理科数学试卷(解析版) 题型:填空题
设m为实数,若{(x,y)| ⊆{(x,y)|(x-2)2+(y-2)2≤8},则m的取值范围为________.
⊆{(x,y)|(x-2)2+(y-2)2≤8},则m的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com