
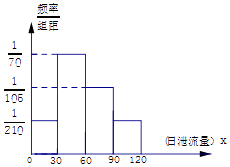
����Ŀ��ij�������ڸõ�һˮ���Ͻ���һ��ˮ��վ����й��ˮ�����磬��ͼ�Ǹ��ݸ�ˮ���������й������ˮ�����ϻ��ɵ���й����X����λ���������ף���Ƶ�ʷֲ�ֱ��ͼ��������������֪X��[0��120]����������й����������[30��60������ƽ������Ϊ156�죬һ�갴364��ƣ� 
��1�����Ƶ��ֱ��ͼ����������
��2����ˮ��վϣ����װ�ķ�������������У���ÿ30����������й�������ܹ�����һ̨���������60��X��90ʱ�Ź�������̨�������������һ̨�������ÿ��ɻ�����4000Ԫ���������У����̨�����ÿ�����500Ԫ���Ը��ε�Ƶ����Ϊ��Ӧ�εĸ��ʣ���ˮ��վ�����������ֵΪ�������ݣ��ʣ�Ϊʹˮ��վ�����������ֵ���ˮ��վӦ��װ����̨�������
���𰸡�
��1���⣺������[30��60����Ƶ��Ϊ ![]() ��
��
![]() =
= ![]() =
= ![]() ��
��
��������[0��30���ϣ� ![]() =a��
=a��
��a+ ![]() ����30=1��
����30=1��
���a= ![]() ��
��
����Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
��2���⣺��ˮ��վ������ΪYԪ���ɣ���֪���������з�����ĸ���Ϊ ![]() ��
��
ǡ������һ̨������ĸ���Ϊ ![]() ��ǡ�����ж�̨������ĸ���Ϊ
��ǡ�����ж�̨������ĸ���Ϊ ![]() ��
��
ǡ��������̨������ĸ���Ϊ ![]() ��
��
������װ1̨���������Y��ֵΪ��500��4000����ֲ���Ϊ��
Y | ��500 | 4000 |
P |
|
|
E��Y��=��500�� ![]() +4000��
+4000�� ![]() =
= ![]() ��
��
������װ2̨���������Y��ֵΪ��1000��3500��8000����ֲ���Ϊ��
Y | ��1000 | 3500 | 8000 |
P |
|
|
|
E��Y��=��1000�� ![]() +3500��
+3500�� ![]() +8000��
+8000�� ![]() =
= ![]() ��
��
������װ3̨���������Y��ֵΪ��1500��3000��7500��12000����ֲ���Ϊ
Y | ��1500 | 3000 | 7500 | 12000 |
P |
|
|
|
|
E��Y��=��1500�� ![]() +3000��
+3000�� ![]() +7500��
+7500�� ![]() +12000��
+12000�� ![]() =
= ![]() ��
��
�� ![]() ��
��
��Ҫʹˮ��վ�����������ֵ���ˮ��վӦ��װ3̨�������
��������������������[0��30���ϣ� ![]() =a����Ƶ�ʷֲ�ֱ��ͼ���������a=
=a����Ƶ�ʷֲ�ֱ��ͼ���������a= ![]() ���ɴ��ܲ�������Ƶ�ʷֲ�ֱ��ͼ������ˮ��վ������ΪYԪ���������з�����ĸ���Ϊ
���ɴ��ܲ�������Ƶ�ʷֲ�ֱ��ͼ������ˮ��վ������ΪYԪ���������з�����ĸ���Ϊ ![]() ��ǡ������һ̨������ĸ���Ϊ
��ǡ������һ̨������ĸ���Ϊ ![]() ��ǡ�����ж�̨������ĸ���Ϊ
��ǡ�����ж�̨������ĸ���Ϊ ![]() ��ǡ��������̨������ĸ���Ϊ
��ǡ��������̨������ĸ���Ϊ ![]() ���ֱ������װ1̨���������װ2̨���������װ3̨���������ѧ�������ɴ˵õ�Ҫʹˮ��վ�����������ֵ���ˮ��վӦ��װ3̨�������
���ֱ������װ1̨���������װ2̨���������װ3̨���������ѧ�������ɴ˵õ�Ҫʹˮ��վ�����������ֵ���ˮ��վӦ��װ3̨�������
�����㾫����������Ĺؼ���������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC����x�� ![]() ��2+��y��1��2=1������A����t��0����B��t��0����t��0������ԲC�ϴ��ڵ�P��ʹ�á�APB=90�㣬��tȡ�����ֵʱ����P�������ǣ� ��
��2+��y��1��2=1������A����t��0����B��t��0����t��0������ԲC�ϴ��ڵ�P��ʹ�á�APB=90�㣬��tȡ�����ֵʱ����P�������ǣ� ��
A.�� ![]() ��
�� ![]() ��
��
B.�� ![]() ��
�� ![]() ��
��
C.�� ![]() ��
�� ![]() ��
��
D.�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㾭�����ҹ��ϱ���ʱ�ڵ�һ����Ҫ��ѧ����������ϵͳ�Ľ����˵Ȳ����У�ͬ���������ٶ�����ӡ�Ȳ��״γ��֣�����������һ�����⣬����Ϊ��ijŮ������֯������һ���ǰһ��֯�Ŀ죬����ÿ�����ӵ�������ͬ����֪��һ��֯��5�ߣ�һ���£���30����㣩�ܹ�֯��390�ߣ���ÿ�����ӵ�����Ϊ���ٳߣ�������Ĵ�Ϊ�� ��
A.![]() ��
��
B.![]() ��
��
C.![]() ��
��
D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����c=2 ![]() ��sinB=2sinA��
��sinB=2sinA��
��1����C= ![]() ����a��b��ֵ��
����a��b��ֵ��
��2����cosC= ![]() �����ABC�������
�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p���������� ![]() ��
�� ![]() ��ʹ��
��ʹ�� ![]()
![]() =|
=| ![]() ||
|| ![]() |������q�������������
|������q������������� ![]() ��
�� ![]() ��
�� ![]() ����
���� ![]()
![]() =
= ![]()
![]() ����
���� ![]() =
= ![]() ���������ж���ȷ���ǣ� ��
���������ж���ȷ���ǣ� ��
A.����p��q�Ǽ�����
B.����p��q��������
C.����p�ţ��Vq���Ǽ�����
D.����p�ģ��Vq����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��߳�Ϊ6cm��������ֽƬ���Ȱ���ͼ1��ʾ����Ӱ���ֽ�ȥ�ĸ�ȫ�ȵĵ��������Σ�Ȼ��ʣ�ಿ���������۵���ƴ��һ��������ģ�ͣ������������Σ��Ӷ�������������ߣ������ǵ������ĵ�������������������ͼ2���ã���������ͼΪ�������Σ��������Ϊcm3 �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ![]() Ϊʵ��������
Ϊʵ�������� ![]() �ĵ�����Ϊ
�ĵ�����Ϊ ![]() ����
���� ![]() ��ż������ �����ߣ�
��ż������ �����ߣ� ![]() �ڵ�
�ڵ� ![]() �������߷���Ϊ�� ��
�������߷���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��G��x��=xlnx+��1��x��ln��1��x����
��1����G��x������Сֵ��
��2����G��x������СֵΪe����֪����f��x��=2aex+1+ ![]() ��2��a+1����a��0���������������x�ʣ�0��+�ޣ�������f��x����0��������ʵ��a��ȡֵ��Χ��
��2��a+1����a��0���������������x�ʣ�0��+�ޣ�������f��x����0��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�м����д����ϣ���Ҫ���ܱ��мס������ҵ���̨���ߵ����ʣ����ҵ���̨���м���5�ˣ���������Ҫ����10��������ѡ��4���������ʣ�����4���У����м�̨���ߣ������ҵ���̨���ߣ��Ҽ���̨�ļ��߲������������ʣ���ͬ�����ʷ�ʽ������Ϊ�� ��
A.1200
B.2400
C.3000
D.3600
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com