Question

将平面上的每个点都以红，蓝两色之一着色．证明：存在这样两个相似的三角形，它们的相似比为1995，并且每一个三角形的三个顶点同色．

Answer 1

【答案】分析：法一：首先证明平面上一定存在三个顶点同色的直角三角形，再把三角形补成矩形，把矩形的每边都分成n等分（n为正奇数，n＞1，本题中取n=1995），连接对边相应分点，把矩形ABCD分成n²个小矩形．即可得到结论；
法二：以任一点O为圆心，a及1995a为半径作两个同心圆，在小圆上任取9点，必有5点同色，作射线交大圆于五点，则此五点中必存在三点同色，一次可得结论．
解答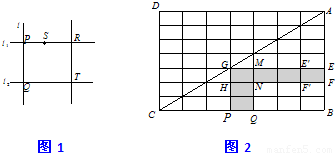：法一：证明：首先证明平面上一定存在三个顶点同色的直角三角形．
任取平面上的一条直线l，则直线l上必有两点同色．设此两点为P、Q，不妨设P、Q同着红色．
过P、Q作直线l的垂线l₁、l₂，
若l₁或l₂上有异于P、Q的点着红色，则存在红色直角三角形；
若l₁、l₂上除P、Q外均无红色点，则在l₁上任取异于P的两点R、S，则R、S必着蓝色，过R作l₁的垂线交l₂于T，则T必着蓝色．△RST即为三顶点同色的直角三角形．
设直角三角形ABC三顶点同色（∠B为直角），把△ABC补成矩形ABCD（如图），把矩形的每边都分成n等分（n为正奇数，n＞1，本题中取n=1995），连接对边相应分点，把矩形ABCD分成n²个小矩形．
AB边上的分点共有n+1个，由于n为奇数，故必存在其中两个相邻的分点同色，（否则任两个相邻分点异色，则可得A、B异色），不妨设相邻分点E、F同色．
考察E、F所在的小矩形的另两个顶点E′、F′，若E′、F′异色，则△EFE′或△DFF′为三个顶点同色的小直角三角形．若E′、F′同色，再考察以此二点为顶点而在其左边的小矩形，…．这样依次考察过去，不妨设这一行小矩形的每条竖边的两个顶点都同色．
同样，BC边上也存在两个相邻的顶点同色，设为P、Q，则考察PQ所在的小矩形，
同理，若P、Q所在小矩形的另一横边两个顶点异色，则存在三顶点同色的小直角三角形，否则，PQ所在列的小矩形的每条横边两个顶点都同色．
现考察EF所在行与PQ所在列相交的矩形GHNM，如上述，M、H都与N同色，△MNH为顶点同色的直角三角形．
由n=1995，故△MNH∽△ABC，且相似比为1995，且这两个直角三角形的顶点分别同色．
法二：以任一点O为圆心，a及1995a为半径作两个同心圆，在小圆上任取9点，必有5点同色，设为A、B、C、D、E，作射线OA、OB、OC、OD、OE，交大圆于A′，B′，C′，D′，E′，则此五点中必存在三点同色，设为A′、B′、C′．则△ABC与△A′B′C′为满足要求的三角形．
点评：本题考查抽屉原理，考查学生分析解决问题的能力，属于中档题