
【题目】将锐角三角形绕其一边旋转一周所形成的空间几何体是
A. 一个圆柱 B. 一个圆锥 C. 一个圆台 D. 两个圆锥的组合体
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,圆心在
,圆心在![]() 上.
上.
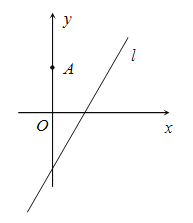
(Ⅰ)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(Ⅱ)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置, 指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右下表.
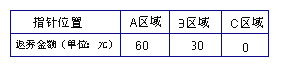

例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)已知顾客甲消费后获得![]() 次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为
次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为![]() ,每次转动转盘的结果相互独立,设
,每次转动转盘的结果相互独立,设![]() 为顾客甲转动转盘指针落在区域边界的次数,
为顾客甲转动转盘指针落在区域边界的次数,![]() 的数学期望
的数学期望![]() ,方差
,方差![]() .求
.求![]() 、
、![]() 的值;
的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com