
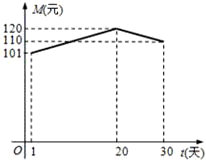
 经市场调查分析,某旅游城市在上月内(以30天计算),第t天旅游人数S(万人)与时间t满足:S-4与t成反比,且上月第20天旅游人数为4.05万人,又第t天旅游人均消费M(元)与时间t的关系如图所示.
经市场调查分析,某旅游城市在上月内(以30天计算),第t天旅游人数S(万人)与时间t满足:S-4与t成反比,且上月第20天旅游人数为4.05万人,又第t天旅游人均消费M(元)与时间t的关系如图所示. ,
, .
.
 =
=

 时取到等号.
时取到等号. ,
, 在21≤t≤30,t∈N是单调递减,
在21≤t≤30,t∈N是单调递减, .
. ,得t2-20t+25≥0,
,得t2-20t+25≥0, ,所以t=19,20,1.
,所以t=19,20,1. ,得2t2-39t-70≤0,
,得2t2-39t-70≤0, ,所以t=21.
,所以t=21. ,将t=20,S=4.05代入,求出k,根据图象求出M,从而根据旅游日收益=日旅游人数×日旅游人均消费求出旅游日收益;
,将t=20,S=4.05代入,求出k,根据图象求出M,从而根据旅游日收益=日旅游人数×日旅游人均消费求出旅游日收益;

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:单选题
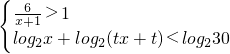 的解集构成的各区间的长度和为5,则实数t的取值范围是
的解集构成的各区间的长度和为5,则实数t的取值范围是查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图在直三棱柱ABC-A1B1C1中,棱AB,BC,BB1两两垂直长度相等,点P在线段A1C1上运动,异面直线BP与B1C所成的角为θ,则θ的取值范围是________.
如图在直三棱柱ABC-A1B1C1中,棱AB,BC,BB1两两垂直长度相等,点P在线段A1C1上运动,异面直线BP与B1C所成的角为θ,则θ的取值范围是________.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个 小洞D、E、F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛永的体积是原来的
如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个 小洞D、E、F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛永的体积是原来的查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com