
(Ⅰ)(坐标系与参数方程)直线 与圆
与圆 相交的弦长为 .
相交的弦长为 .
(Ⅱ)(不等式选讲)设函数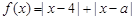
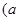 >1),且
>1),且 的最小值为
的最小值为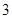 ,若
,若 ,则
,则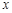 的取值范围
的取值范围
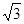 (Ⅱ)
(Ⅱ)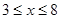
【解析】
试题分析:解:将直线2ρcosθ=1化为普通方程为:2x=1.∵ρ=2cosθ,∴ρ2=2ρcosθ,化为普通方程为:x2+y2=2x,即(x-1)2+y2=1.∴直线与圆相交的弦长=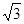
解:∵函数f(x)=|x-4|+|x-a|≥|x-4+a-x|=|a-4|,∵f(x)的最小值为3,∴|a-4|=3,∴a=1或7,∵a>1,∴a=7,∴f(x)=|x-4|+|x-7|≤5,①若x≤4,f(x)=4-x+7-x=11-2x≤5,解得x≥3,故3≤x≤4;②若4<x<7,f(x)=x-4+7-x=3,恒成立,故4<x<7;③若x≥7,f(x)=x-4+x-7=2x-11≤5,解得x≤8,故7≤x≤8;
综上3≤x≤8,故答案为:3≤x≤8.
考点:坐标系与参数方程,不等式选讲
点评:主要是考查了不等式选讲以及坐标系与参数方程的运用,属于基础题。


科目:高中数学 来源: 题型:
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲 |
| AB |
|
|
|
|
|
|
| n(2n-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com