
【题目】已知a2 , a5是方程x2﹣12x+27=0的两根,数列{an}是公差为正的等差数列,数列{bn}的前n项和为Tn , 且Tn=1 ![]() bn . (n∈N*)
bn . (n∈N*)
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)记cn=anbn , 求数列{cn}的前n项和Sn .
【答案】解:(Ⅰ)由题意可得:a2+a5=12,a2a5=27,且d>0,
解得:a2=3,a5=9,
∴ ![]() ,
,
则an=3+2(n﹣2)=2n﹣1;
在Tn=1 ![]() bn中,令n=1,得
bn中,令n=1,得 ![]() ;
;
当n≥2时, ![]() ,
,
得 ![]() ,
,
∴ ![]() (n≥2),
(n≥2),
∴ ![]() ;
;
(Ⅱ)cn=anbn= ![]() ,
,
∴ ![]() ,
,
![]() ,
,
∴ ![]() =2[
=2[ 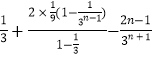 ]
]
= ![]() =
= ![]() ,
,
∴ ![]()
【解析】(Ⅰ)由韦达定理可求出a2=3,a5=9,进而求出等差数列的公差d,故得出通项公式。再利用Tn和 b n的关系可推导出{bn}的通项公式。(Ⅱ)
整理cn 的通向公式,得出 S n的等式,在两边乘以公比转化成除去首末两项的一个等比数列,再由等比数列求和公式求出结果。
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系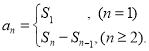 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(﹣1,0),B(1,1),C(2,0),点P是平面直角坐标系xOy上一点,且 ![]() =m
=m ![]() (m,n∈R),
(m,n∈R),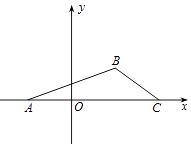
(1)若m=1,且 ![]() ∥
∥ ![]() ,试求实数n的值;
,试求实数n的值;
(2)若点P在△ABC三边围成的区域(含边界)上,求m+3n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(1+x)+alog2(1﹣x)(a∈R)的图象关于y轴对称.
(1)求函数f(x)的定义域;
(2)求a的值;
(3)若函数g(x)=x﹣2f(x)﹣2t有两个不同的零点,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①f(x)=sin(2x﹣ ![]() )的对称轴为x=
)的对称轴为x= ![]() ,k∈Z;②若函数y=2cos(ax﹣
,k∈Z;②若函数y=2cos(ax﹣ ![]() )(a>0)的最小正周期是π,则a=2;③函数f(x)=sinxcosx﹣1的最小值为﹣
)(a>0)的最小正周期是π,则a=2;③函数f(x)=sinxcosx﹣1的最小值为﹣ ![]() ;④函数y=sin(x+
;④函数y=sin(x+ ![]() )在[﹣
)在[﹣ ![]() ]上是增函数,其中正确命题的个数是( )
]上是增函数,其中正确命题的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() sin(2x+φ)(|φ|<
sin(2x+φ)(|φ|< ![]() )的图象关于直线x=
)的图象关于直线x= ![]() 对称,且当x1 , x2∈(﹣
对称,且当x1 , x2∈(﹣ ![]() ,﹣
,﹣ ![]() ),x1≠x2时,f(x1)=f(x2),则f(x1+x2)等于( )
),x1≠x2时,f(x1)=f(x2),则f(x1+x2)等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 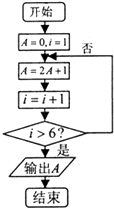
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com