练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （22）已知函数且存在使

    （I）证明：是R上的单调增函数；

    （II）设

    其中　

    证明：

    （III）证明：

    解：(1)∵f′(x)=3x2－2x+=3(x－)2+＞0,    ∴f(x)是R上的单调增函数.

    （Ⅱ）∵0＜x0＜,  即  x1＜x0＜y1.   又f(x)是增函数.  ∴f(x1)＜f(x0)＜f(y1),

    即x2＜x0＜y2,  又   x2=f(x1)=f(0)= ＞0=x1,y2=f(y1)=f()=＜=y1.

    综上，x1＜x2＜x0＜y2＜y1.

    用数学归纳法证明如下：（1）当n=1时，上面已证明成立.

    (2)假设当n=k  (k≥1)时有  xk＜xk+1＜x2＜yk+1＜y2.

    当n=k+1时，由f(x)是单调增函数，有f(xk)＜f(xk+1)＜f(x0)＜f(yk+1)＜f(yk)，

    ∴xk+1＜xk+2＜x0＜yk+2＜yk+1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出以下五个命题，其中所有正确命题的序号为
    ①③
    ①③

    ①函数f(x)=
    		x2-2x
    +2
    		x2-5x+4
    的最小值为l+2
    		2
    ；
    ②已知函数f （x）=|x2-2|，若f （a）=f （b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1；
    ③命题“函数f（x）=xsinx+1，当x1，x2∈[-
    π
    2
    ，
    π
    2
    ]    ，且|x1|＞|x2|时，有f （x1）＞f（x2）”是真命题；
    ④“a=
    ∫
    1
    0
    		1-x2
    dx    ”是函数“y=cos2（ax）-sin2（ax）的最小正周期为4”的充要条件；
    ⑤已知等差数列{an}的前n项和为Sn，
    OA
    ，
    OB
    为不共线向量，又
    OP
    =a
    OA
    +a2012
    OB
    ，若
    PA
    =λ
    PB
    ，则S2012=2013．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分15分）已知函数  且导数.

      （Ⅰ）试用含有的式子表示，并求单调区间;  （II）对于函数图象上的不同两点，如果在函数图象上存在点（其中）使得点处的切线，则称存在“伴侣切线”.特别地，当时，又称存在“中值伴侣切线”.试问：在函数上是否存在两点、使得它存在“中值伴侣切线”，若存在，求出、的坐标，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源：江苏省海门中学2009—2010学年度第二学期期中测试卷高二数学（文科） 题型：解答题

    (本小题满分16分) 
    已知函数且（1）求的单调区间；
    （2）若函数与函数在时有相同的值域，求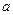的值；
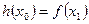    （3）设，函数，若对于任意，总存在，使得 成立，求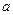的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省高三十一月份阶段性考试理科数学 题型：解答题

    （本题满分14分）

    已知函数且存在使

    （I）证明：是R上的单调增函数；

    （II）设其中　

         证明：

    （III）证明：

     

    查看答案和解析>>

    同步练习册答案