练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知若，且f(x)图像上相邻的两个对称轴的距离是

    (1)求函数f(x)在区间上的最大值和最小值．

    (2)锐角△ABC中，角A、B、C所对的边分别为a，b，c，若求角C．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知ω＞0，向量
    m
    =(1，2cosωx)，
    n
    =(
    		3
    sin2ωx，-cosωx)．设函数f(x)=
    m
    •
    n
    ，且f(x)    图象上相邻的两条对称轴的距离是
    π
    2
    ．
    （I）求ω的值及f（x）的单调递增区间；
    （Ⅱ）若x∈[
    π
    4
    ，
    π
    2
    ]，求函数f(x)    的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源：江西省新建二中2010届高三上学期第一次月考数学理科试题 题型：044

    已知函数，且f(x)与g(x)的函数图象关于直线y＝x对称，又．

    (1)求f(x)的值域；

    (2)是否存在实数m，使得命题p：f(m2－m)＜f(3m－4)和q：g满足复合命题“p且q”为真命题？若存在，求出m的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f(x)=ax2+bx+c的图象过A（t1,y1）、B(t2,y2)两点，且满足a2+(y1+y2)a+y1y2=0.

    (1)证明：y1=-a或y2=-a;

    (2)证明：函数f(x)的图像必与x轴有两个交点;

    (3)若关于x的不等式f(x)＞0的解集为{x|x＞m或x＜n}（n＜m＜0），解关于x的不等式cx2-bx+a＞0.

    查看答案和解析>>

    科目：高中数学 来源：2012年四川省泸州市高考数学一诊试卷（理科）（解析版） 题型：解答题

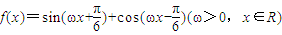    已知函数，且该函数图象相邻两对称轴间的距离为．
    （I）求函数f（x）的解析式；
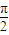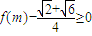    （II）若不等式成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2014届山西省高一下学期月考数学试卷 题型：解答题

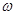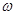    已知函数f(x)＝sinx(＞0).

    （1）若y＝f(x)图象过点(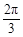，0)，且在区间(0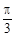，)上是增函数，求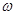的值.

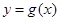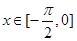    （2）先把（1）得到的函数y＝f(x)图象上各点的纵坐标伸长为原来的2倍，（横坐标不变）；再把所得的图象向右平移个单位长度，设得到的图象所对应的函数为，求当时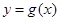，的最大和最小值

     

    查看答案和解析>>

    同步练习册答案