
已知函数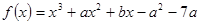 在
在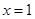 处取得极大值
处取得极大值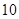 ,则
,则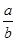 的值为( )
的值为( )
A. | B.-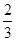 | C.-2或一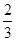 | D.不存在 |
B
解析试题分析::∵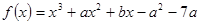 ,∴f′(x)=3x2+2ax+b,
,∴f′(x)=3x2+2ax+b,
又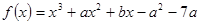 在x=1处取得极大值10,
在x=1处取得极大值10,
∴f′(1)=3+2a+b=0,f(1)=1+a+b-a2-7a=10,
∴a2+8a+12=0,
∴a=-2,b=1或a=-6,b=9.
当a=-2,b=1时,f′(x)=3x2-4x+1=(3x-1)(x-1),
当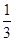 <x<1时,f′(x)<0,当x>1时,f′(x)>0,
<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在x=1处取得极小值,与题意不符;
当a=-6,b=9时,f′(x)=3x2-12x+9=3(x-1)(x-3),
当x<1时,f′(x)>0,当<x<3时,f′(x)<0,
∴f(x)在x=1处取得极大值,符合题意;
∴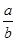 =-
=-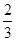 ,故选B。
,故选B。
考点:利用导数研究函数的极值。
点评:中档题,函数的极值点处的导数值为0.本题解答中,a,b有两组解,注意检验验证,合理取舍。


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:单选题
已知函数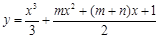 的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数
的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数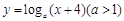 的图象上存在区域D内的点,则实数a的取值范围为( )
的图象上存在区域D内的点,则实数a的取值范围为( )
A.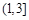 | B.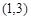 | C. | D.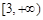 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com