一次掷硬币游戏,共有六位学生参加.游戏规定每位学生都将一枚均匀的硬币连抛两次,并记录结果.若两次中至少有一次正面向上,则称该同学抛掷成功,否则称抛掷失败.求:
(I)六名学生中的某学生甲抛掷成功的概率;
(II)抛掷成功的人数不少于失败的人数的概率;
(III)抛掷成功的人数ξ的数学期望.
【答案】
分析:(I)由已知中游戏规定每位学生都将一枚均匀的硬币连抛两次,并记录结果.若两次中至少有一次正面向上,则称该同学抛掷成功,否则称抛掷失败.我们列出所有情况的基本事件个数,及满足条件甲抛掷成功的基本事件个数,然后代入古典概型公式,即可得到答案.
(II)抛掷成功的人数不少于失败的人数是抛掷成功的人数少于失败的人数,计算出抛掷成功的人数少于失败的人数的概率,然后利用对立事件概率减法公式,即可求出抛掷成功的人数不少于失败的人数的概率;
(III)每名学生抛掷成功的概率均相等,且每名学生抛掷成功的概率均为

,代入数学期望公式,即可得到答案.
解答:解:(1)每位学生都将一枚均匀的硬币连抛两次,
结果共有(正,正),(正,反),(反,正),(反,反)4种,
其中该同学抛掷成功的情况有(正,正),(正,反),(反,正)三种
∴学生甲抛掷成功的概率
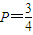
(4分)
(II)抛掷成功的人数不少于失败的人数是抛掷成功的人数少于失败的人数共包括如下几种情况:
六名学生都失败,概率为
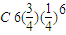
五名学生失败,一名学生成功,概率为
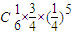
四名学生失败,二名学生成功,概率为
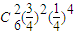
故抛掷成功的人数不少于失败的人数的概率
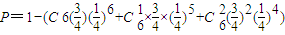
=
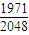
(8分)
(III)∵每名学生抛掷成功的概率均相等
且每名学生抛掷成功的概率均为

∴
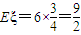
(12分)
点评:本题考查的知识点是n次独立重复试验中恰好发生k次的概率,相互独立事件的概率乘法公式及离散型随机变量的期望,其中熟练掌握n次独立重复试验中恰好发生k次的概率公式是解答本题的关键.

 ,代入数学期望公式,即可得到答案.
,代入数学期望公式,即可得到答案.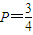 (4分)
(4分)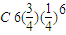
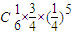
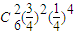
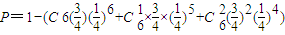 =
= (8分)
(8分)
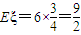 (12分)
(12分)

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案