
(06年上海卷理)(14分)
在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]()
![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
解析:(1)设过点T(3,0)的直线![]() 交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
交抛物线y2=2x于点A(x1,y1)、B(x2,y2).
当直线![]() 的钭率不存在时,直线
的钭率不存在时,直线![]() 的方程为x=3,此时,直线
的方程为x=3,此时,直线![]() 与抛物线相交于点A(3,
与抛物线相交于点A(3,![]() )、B(3,-
)、B(3,-![]() ). ∴
). ∴![]() =3;
=3;
当直线![]() 的钭率存在时,设直线
的钭率存在时,设直线![]() 的方程为
的方程为![]() ,其中
,其中![]() ,
,
由![]() 得
得 ![]()
又 ∵ ![]() ,
,
∴![]() ,
,
综上所述,命题“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]() =3”是真命题;
=3”是真命题;
(2)逆命题是:设直线![]() 交抛物线y2=2x于A、B两点,如果
交抛物线y2=2x于A、B两点,如果![]() =3,那么该直线过点T(3,0).该命题是假命题.
=3,那么该直线过点T(3,0).该命题是假命题.
例如:取抛物线上的点A(2,2),B(![]() ,1),此时
,1),此时![]() =3,
=3,
直线AB的方程为:![]() ,而T(3,0)不在直线AB上;
,而T(3,0)不在直线AB上;
说明:由抛物线y2=2x上的点A (x1,y1)、B (x2,y2) 满足![]() =3,可得y1y2=-6,
=3,可得y1y2=-6,
或y1y2=2,如果y1y2=-6,可证得直线AB过点(3,0);如果y1y2=2,可证得直线AB过点(-1,0),而不过点(3,0).


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
(06年上海卷理)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
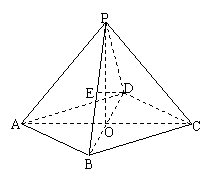
(06年上海卷理)(14分)在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60![]() ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60![]() .
.
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
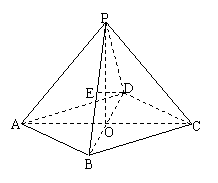
(06年上海卷理)(14分)在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60![]() ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60![]() .
.
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com