
 .假设两种种子是否发芽互相不受影响,任何两粒种子是否发芽互相也没有影响.
.假设两种种子是否发芽互相不受影响,任何两粒种子是否发芽互相也没有影响.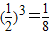 ,
,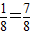
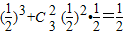 ,
, ,
, ,
,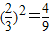 ,
, ,
,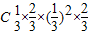 =
=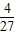 ,
,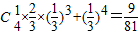 ,
,
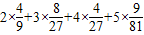 =
=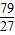


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某生物兴趣小组对A、B两种植物种子的发芽率进行验证性实验,每实验一次均种下一粒A种子和一粒B种子.已知A、B两种种子在一定条件下每粒发芽的概率分别为![]() .假设两种种子是否发芽互相不受影响,任何两粒种子是否发芽互相也没有影响。
.假设两种种子是否发芽互相不受影响,任何两粒种子是否发芽互相也没有影响。
(1)求3粒A种子,至少有一粒未发芽的概率;
(2)求A、B各3粒种子,A至少2粒发芽且B全发芽的概率;
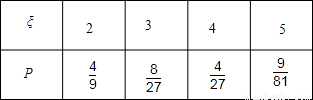
(3)假设对B种子的实验有2次发芽,则终止实验,否则继续进行,但实验的次数最多不超过5次,求对B种子的发芽实验终止时,实验次数![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com