Question

等差数列{a_n}、{b_n}的前n项的和分别为S_n、T_n.

(1)若a_m=n,a_n=m,求a_m+n?和S_m+n?;

(2)若S_m=n,S_n=m(m≠n),求S_m+n?;

(3)若=(n∈N^*),求.

Answer 1

解析:(1)设{a_n}的公差为d.?

方法一:由a_m=n,a_n=m,得?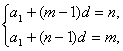

解得?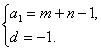

所以a_m+n=a₁+(m+n-1)d=0.?

S_m+n==?

方法二:d==-1.?

a_m+n=a_m+nd=n-n=0.?

同上可得S_m+n=?

(2)由S_m=n,S_n=m(m≠n),?

得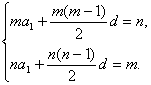

两式相减可得(m-n)a₁+?

又m≠n,所以a₁+ d=-1.?

2a₁+(m+n-1)d=-2.?

故S_m+n= =·［2a₁+(m+n-1)d］=-(m+n).?

(3)方法一:== =?

= =?

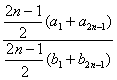方法二:{a_n}为等差数列前n项和S_n=An²+Bn(A、B为常数),?

不妨设S_n=an(7n+1),T_n=an(4n+27)(a≠0且为?常数)?,?

则==

=