
平面上有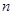 个圆,其中每两个都相交于两点,每三个都无公共点,它们将平面分成
个圆,其中每两个都相交于两点,每三个都无公共点,它们将平面分成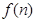 块区域,有
块区域,有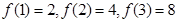 ,则
,则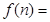 (
)
(
)
A.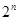 B.
B.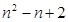
C.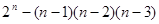 D.
D.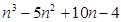
B
【解析】
试题分析:∵ f(1)
=" 2" ;假设已经有k个圆,将平面分成了 f(k)
部分,当第 k+1 个圆参与近来时,它与前 k 个圆总共产生 2k 个交点 ,这 2k 个交点将此圆分成 2k 段弧,这 2k 段弧中的每一段都将其所在的原来的一片区域一分为二,故总共增加了 2k 个部分,即 f(k+1)
=" f(k)" + 2k ,即f(k+1) -
f(k) = 2k ,由 f(1) = 2, f(2) -
f(1) = 2,f(3) - f(2) = 4, f(4) - f(3) = 6,.................f(n) - f(n-1) = 2(n-1),以上各式相加,得f(n) =" 2" + 2 + 4 + 6 + ..... + 2(n-1) =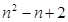 。故选B,本题也可用代入检验法
。故选B,本题也可用代入检验法
考点:本题考查了归纳推理的运用
点评:熟练掌握归纳推理的概念是解决此类问题的关键


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com