
 ,若关于x的函数
,若关于x的函数 有5个不同的零点x1,x2,x3,x4,x5,则x12+x22+x32+x42+x52等于( )
有5个不同的零点x1,x2,x3,x4,x5,则x12+x22+x32+x42+x52等于( )
 有5个不同的实数解x1,x2,x3,x4,x5,则必有f(x)=1这个等式,由根与系数的关系得另一个根是f(x)=
有5个不同的实数解x1,x2,x3,x4,x5,则必有f(x)=1这个等式,由根与系数的关系得另一个根是f(x)= ,从而可得5个根的平方和,问题得到解决.
,从而可得5个根的平方和,问题得到解决.
 =0有5个不同的实数解:
=0有5个不同的实数解: ,
,

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
|
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市徐汇区位育中学高三(上)期中数学试卷(文科)(解析版) 题型:填空题
 ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .查看答案和解析>>
科目:高中数学 来源:2013年上海市长宁、嘉定区高考数学二模试卷(理科)(解析版) 题型:填空题
 ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .查看答案和解析>>
科目:高中数学 来源:2014届四川省成都市六校协作体高一下学期期中联考数学试卷(解析版) 题型:选择题
已知定义域为R的函数 ,若关于
,若关于 的方程
的方程 有3个不同的实根,则关于x的不等式
有3个不同的实根,则关于x的不等式 的解集为( )
的解集为( )
A.(2,c)
B.(c,2) C. (1,c)  D. (c,1)
D. (c,1)
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学文史类模拟试卷(三) 题型:选择题
已知定义域为R的函数 ,若关于
,若关于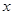 的方程
的方程 有3个不同的实根
有3个不同的实根 ,则
,则 等于
等于
A.
5 B.  C. 13 D.
C. 13 D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com