
正四棱锥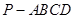 中,
中,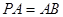 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且 .
.

(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证: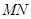 ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.
(1)90o
(2)要证明线面平行,则主要证明线线平行即可,结合判定定理得到。
(3)
【解析】
试题分析:(Ⅰ)设AC与BD的交点为O,AB=PA=2。以点O为坐标原点, ,
, 方向分别是x轴、y轴正方向,建立空间直角坐标系O-xyz.
方向分别是x轴、y轴正方向,建立空间直角坐标系O-xyz.
则A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),
设P(0,0,p), 则 =(-1,1,p),又AP=2,∴1+1+p2=4,∴p=
=(-1,1,p),又AP=2,∴1+1+p2=4,∴p= ,
,
∵ =
= ,
,
 ,
,
∴ ,
, ,
,
∵ ,∴异面直线MN与AD所成角为90o
,∴异面直线MN与AD所成角为90o
(Ⅱ)∵ ,
,
设平面PBC的法向量为 ="(a,b,c),"
="(a,b,c),"
 则
则 ,
,
取 =
= , ∵
, ∵ ,∴MN∥平面PBC。
,∴MN∥平面PBC。
(Ⅲ)设平面PAB的法向量为 ="(x,y,z),"
="(x,y,z),"

由 ,∴
,∴ 则
则 ,
,
取 =
= , cos<
, cos< > =
> = ,
,
∴MN与平面PAB所成角的正弦值是

考点:线面平行和线面角的求解
点评:主要是考查了线面的位置关系的运用,属于中档题。


科目:高中数学 来源: 题型:
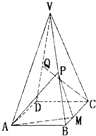 (2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2
(2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,正四棱锥![]() 中,
中,![]() ,
,
点M,N分别在PA,BD上,且![]() .
.
(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证:![]() ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.
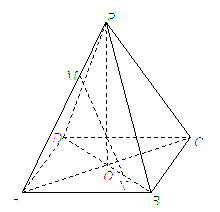
查看答案和解析>>
科目:高中数学 来源:2012届江苏省第一学期期末考试高二数学试题 题型:解答题
正四棱锥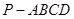 中,
中, ,
,
点M,N分别在PA,BD上,且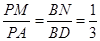 .
.
(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证: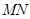 ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com