Question

下图是一人出差从A城出发到B城去，沿途可能经过的城市的示意图，通过两城市所需时间标在两城市之间的连线上（单位:h），试求此人从A城出发到B城所需时间最少要多少小时？

Answer 1

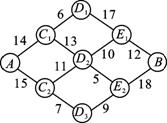
思路分析：如果从A开始逐一计算所有可能的路线所需的时间，工作量显然较大，且易出现遗漏.注意到最优路线图中的某一城市必存在这样的事实：不管前面的路线如何，从本城市出发到终点的路线耗时仍然是最短的，否则就会存在耗时更短的路线，产生与最优路线的假设相矛盾.这就启示我们可以从终点B出发，倒溯着局部选择耗时最短的最优路线.

解：设各城市至B城市所需时间的最短时间为S(x)，x为城市记号，则S(E₁)=12,S(E₂)=18,S(D₁)=17+S(E₁)=29,S(D₂)=min{10+S(E₁),5+S(E₂)}=22,S(D₃)=9+S(E₂)=27,S(C₁)=min{6+S(D₁),13+S(D₂)}=35,S(C₂)=min{11+S(D₂),7+S(D₃)}=33,S(A)=min{14+S(C₁),15+S(C₂)}=48.故从A城到B城所需时间最少为48 h,其最短的路线是A—C₂—D₂—E₁—B.