
(1)用rk表示ak;
(2)用rk-1表示rk;
(3)若a1<0,半圆C1和y轴相切,求r1;
(4)在(3)中的半圆C1是这一系列半圆的左起第一个半圆,面积为S1,第k个半圆的面积为Sk,求S1+S2+S3+…+Sk+….
思路解析:这是一个圆与数列相结合的综合题,首先根据半圆与半圆的相切找到几个量之间的关系,根据关系判断数列的类型,再根据数列的类型,完成求和等内容.
解:(1)由题设条件,得直线l的方程为3x+4y-4=0.
圆心到直线的距离
d=rk=![]() .所以ak=
.所以ak=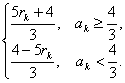
(2)连结ACk,BCk-1,其中A、B分别为圆Ck与圆Ck-1与l的切点,作CkD⊥Ck-1B,则ABDCk是矩形.
kAB=kCD=-![]() ,所以
,所以![]() .
.
故rk=![]() rk-1.
rk-1.
(3)因为a1<0,r1>0,所以r1=-a1.
由点到直线的距离公式可得r1=![]() .
.
所以r1=2.
(4)由(2)可得rk=![]() rk-1,r1=2,
rk-1,r1=2,
所以r1,r2,…,rk,…构成公比为![]() 的等比数列.
的等比数列.
又S1=![]() πr12=2π,S2=
πr12=2π,S2=![]() π,S3=
π,S3=![]() π,可知S1,S2,…,Sk…构成公比为
π,可知S1,S2,…,Sk…构成公比为![]() <1的等比数列.
<1的等比数列.
所以S1+S2+S3+…+Sk+…=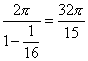 .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com