
| n-1 |
 |
| i=1 |
| n |
| n-i |
| 1 |
| 2i-1 |
| 10 |
| 3 |
| n-1 |
 |
| i=1 |
| n |
| n-i |
| 1 |
| 2i-1 |
| 2 |
| 2-1 |
| 1 |
| 21-1 |
| 10 |
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |
| k+1 |
| k |
| k+1 |
| k-1 |
| 1 |
| 2 |
| k+1 |
| k-2 |
| 1 |
| 22 |
| k+1 |
| 1 |
| 1 |
| 2k-1 |
| k+1 |
| k |
| k+1 |
| 2k |
| k |
| k-1 |
| k |
| k-2 |
| 1 |
| 2 |
| k |
| 1 |
| 1 |
| 2k-2 |
| k+1 |
| k |
| k+1 |
| 2k |
| k+1 |
| k |
| 10 |
| 3 |
| k+1 |
| 2k |
| k+1 |
| k |
| 8 |
| 3 |
| 6 |
| 5 |
| 8 |
| 3 |
| ||
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| m | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013年普通高等学校招生全国统一考试重庆卷理数学 题型:044
对正整数n,记Im={1,2,3,…,n},![]() .
.
(1)求集合P7中元素的个数;
(2)若Pm的子集A中任意两个元素之和不是整数的平方,则称A为“稀疏集”.求n的最大值,使Pm能分成两人上不相交的稀疏集的并.
查看答案和解析>>
科目:高中数学 来源:江苏省扬州中学2012届高三最后冲刺热身数学试题 题型:044
对于正整数n≥2,用Tn表示关于x的一元二次方程x2+2ax+b=0有实数根的有序数组(a,b)的组数,其中a,b∈{1,2,…,n}(a和b可以相等);对于随机选取的a,b∈{1,2,…,n}(a和b可以相等),记Pn为关于x的一元二次方程x2+2ax+b=0有实数根的概率.
(1)求![]() 和
和![]() ;
;
(2)求证:对任意正整数n≥2,有![]() .
.
查看答案和解析>>
科目:高中数学 来源:2013年重庆市高考数学试卷(理科)(解析版) 题型:解答题
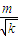 |m∈In,k∈In}.
|m∈In,k∈In}.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com