
已知函数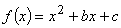 对任意
对任意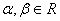 都有
都有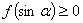 ,且
,且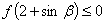 .
.
(1)求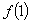 的值;
的值;
(2)求证: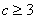 .
.
(3)若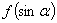 的最大值为10,求
的最大值为10,求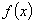 的表达式.
的表达式.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
下列说法中正确的是
A.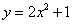 中的
中的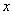 ,
,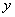 是具有相关关系的两个变量
是具有相关关系的两个变量
B.正四面体的体积与其棱长具有相关关系
C.电脑的销售量与电脑的价格之间是一种确定性的关系
D.某地区感染流感人数与外来流感患者人数是具有相关关系的两个变量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com